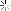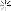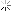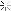-
 مدیر بازنشسته
مدیر بازنشسته
 مطالب مهم و جالب در مورد رياضي
مطالب مهم و جالب در مورد رياضي
با گذشترياضيات مختص فيزيك چيست ؟رياضيات مختص فيزيك ، رياضياتي انحصاري ميباشد كه صرفا در خدمت فيزيك بوده و نميتواند از قواعد فيزيكي عدول كند .
رياضيات مختص فيزيك چيست ؟
همانطور كه ميدانيم رياضيات و فيزيك رابطه تنگاتنگي با هم دارند ، براي اينكه مقوله رياضيات براي انسان ، از شمارش موجودات هستي شروع شده و سيستم شمارش اعداد به تعداد انگشتان دو دست بوده است ( يعني مبناي دهدهي ) ، در واقع راهبرد انسان در رياضيات مقايسه تعداد اشيا با تعداد انگشتان دو دست است يعني يك حرفه دستي كه امروزه مكانيزه و ماشيني شده است . امروزه دو شاخه رياضيات و فيزيك جزء علوم پايه محسوب ميشوند و متاسفانه چون از هم جدا شده و هركدام به صورت حرفهاي و انحصاري دنبال ميشوند ، در پارهاي از موارد مشاهده ميشود كه اين دو علم فاصلهاي از هم گرفته و در بعضي از موارد سر ناسازگاري با هم گذاشته و تناقضهايي مابين آن دو ديده ميشود . در اين مبحث سعي ميكنيم كه اين دو شاخه جدا شده را پيوندي تازه زنيم و اين دو را با هم آشتي قهر ناپذير داده ، همراه و هم سو كنيم و به وسيله اين دو ، كليه پديدههاي موجود در عالم را توجيه نماييم ، البته تا حد توان و مقدوراتمان . رياضيات مختص فيزيك ، رياضياتي انحصاري ميباشد كه صرفا در خدمت فيزيك بوده و نميتواند از قواعد فيزيكي عدول كند . و به قول دكارت " بعد از تحقيق بسيار دريافتم كه در علم رياضيات ، شما با مسايل مربوط به ترتيب و مقدار درگير هستيد و براي شما هيچ فرقي ندارد كه اين مقدار مربوط به ستارگان باشد يا هر شكل ديگري . بنابراين بايد علمي وجود داشته باشد كه هر پرسشي مربوط به ترتيب و مقدار را پاسخ گويد ، بدون توجه به آنكه راجع به ترتيب يا مقدار چه چيزي صحبت ميكند . من اين علم را رياضيات عام مينامم ."
دستگاههاي شمار !
شمارش : اگر هر دست ما بهجاي 5 انگشت 4 انگشت داشت ، چه چيزهايي در زندگي روزمرهمان تغيير ميكرد ؟
ما بهطور معمول براي شمردن ، دستههاي دهتايي درست ميكنيم . ابتدا با 10 تا يكي - 1 بسته دهتايي ، با 10 بسته دهتايي - يك بسته صدتايي و با 10 صدتايي يك بسته هزارتايي درست ميكنيم و به همين ترتيب ، دستهبندي دهتايي را ادامه ميدهيم . نماد 215 نشان ميدهد كه 215 شيء را ميتوانيم در 2 بسته صدتايي ، 1 بسته دهتايي و پنج يكي قرار دهيم . سيستم شمارش اعداد بر مبناي 10 به دستگاه شمار هندو - عربي شهرت يافته است . گرچه مفيد بودن انگشتان در نمايش اعداد به توسعه وسيعي از سيستمي از اعداد كه بر مبناي ده قرار دارد منجر شده است ، ليكن عدد ده به هيچ وجه تنها پايه به كار رفته براي سيستم اعداد نمیباشد . سيستم شمارش بابليها تركيبي از مبناهاي ده و شصت را مورد استفاده قرار میداد كه نشانههاي آن امروزه در واحد اندازهگيري زمان و زاويه يعني 60 ثانيه و 60 دقيقه مشهود است ، در گذشتههاي دور عددهاي نجومي در مبناي 60 نوشته ميشد . امروزه در الكترونيك ديجيتال از مبناي دودويي بيشتر استفاده ميشود . در طول تاريخ ثبت شده است كه پيشرفت جامعههاي متمدن با توسعه سيستم شمارش اعداد و نوشتار متن گفتار ( كتابت و كتاب نويسي ) همراه بوده كه چنين بهنظر مي رسد كه همگي ريشه در وحي كتب آسماني و تاريخ اديان داشته است . نشانههايي از سيستمهايي از اعداد بر پايه سه ، چهار ، پنج ، شش ، هشت ، و بيست در ميان سرخ پوستان آمريكاي شمالي پيدا شده است . بعضي شواهد از سيستم اعداد بر پايه دوازده را ميتوان در مثال اينكه هر فوت دوازده اينچ است يا هر شيلينگ انگليسي دوازده پنس و يا اينكه هر سال دوازده ماه است و يا شبانه روز دو تا 12 ساعت است و ... ، ملاحظه كرد . اما در جوامع امروزي بهنظر میرسد كه سيستم اعداد بر پايه ده برنده شده است . البته نه بهعلت وجود مزاياي ذاتي ، بلكه به نظر میرسد كه به سبب وجود ده انگشت دو دست میباشد . عملهاي حساب دهدهي براي ما بهخوبي آشنا هستند . دانش آموز دبستاني جدولهاي جمع و ضرب را براي 9 عدد اصلي و صفر به همراه بعضي قواعد براي نگهداشتن يك رقم از يك عمل به عمل بعد ياد میگيرد و سرانجام با اين قواعد ياد میگيرد كه عملهاي حسابي را روي هر دسته پايان داري از اعداد دهدهي انجام دهد . در سيستمهاي اعداد ديگر ، دسته قواعد مشابه براي حساب وجود دارد . بخش زير اين قواعد را براي سيستم دوجيني ( دوازده تايي ) توصيف میكند .
سيستم دوجيني يا دوازدهتايي :
ما آنچنان به شمارش در سيستم دهدهي عادت كردهايم كه وقتي مي خواهيم از سيستم اعداد متفاوتي استفاده كنيم ، كاملا مشكل است كه بسياري از عادتهاي فكر كردن را ناديده بگيريم . براي اينكه بعضي از اين اشكالات تذكر داده شوند ، ما در باره سيستم دوجيني يا دوازدهتايي بحث میكنيم .
در اين سيستم علامتهاي زير را به عنوان نشانههاي اساسي به كار میبريم .
1 , 2 , 3 , 4 , 5 , 6 ,7 , 8 , 9 , D , E
حرف D به جاي عدد دهدهي 10 و حرف E بهجاي عدد دهدهي 11 میباشد . گيريم براي جلوگيري از اشتباه كردن آنها را با نامهاي دهدهي dec و el بناميم . عدد بعد از el يك دوجين است كه در اين طرز نمايش به صورت 10 نوشته خواهد شد . عدد بعدي ، كه همان عدد سيزده دهدهي است ، به صورت 11 نوشته میشود . از برخي لحاظ بهتر بود كه بهجاي علامتهاي 1 تا 9 نيز نشانههاي كاملا جديدي براي علامتهاي اساسي سيستم دوجيني انتخاب میگرديد . زيرا كاربرد علامتهاي دهدهي قواعد دهدهي را پيشنهاد میكنند كه در سيستم دوجيني صادق نيستند .
براي مثال ، بهجاي قاعده جمع دهدهي شش به اضافه پنج مساوي يازده ، بايد شش به اضافه پنج مساوي el قرار گيرد .
6+5=(يازده دهدهي)=E
قاعده دهدهي شش به اضافه هفت مساوي سيزده ، بايد بوسيله شش به اضافه هفت مساوي يك دوجين و يك تعويض گردد ، يا
6+7=11دوجيني
پس بايد دقت شود كه دوباره به طرز تفكر قواعد دهدهي برنگرديم . براي علامتهاي اساسي حساب دوجيني يك جدول جمع جديد همچنين يك جدول ضرب جديد بايد آموخته شود . براي مثال پنج ضربدر هشت مساوي چهل دهدهي يا سه دوجين و چهار است ، يا
5*8=40=3*12+4=34دوجيني
براي نوشتن اعداد دوجيني به هر اندازه ، سيستم « ارزش محل » را به كار میبريم ، يعني براي تعيين مقدار هر رقم محل آنرا نسبت به مميز دوجيني ( نه مميز دهدهي ) در نظر ميگيريم ، هر محل سمت راست يا سمت چپ مميز دوجيني از لحاظ مقدار از محل مجاور خود به اندازه يك ضريب دوجين متفاوت مي باشد . به طور مثال :
171دهدهي=3+24+144=3+(12*2)+(12*12*1)=123دو� �� �يني
1.61805555555دهدهي=(12/12/5)+(12/7)+1=1.75دوجيني
سيستم دوجيني از بعضي جهات راحتتر از سيستم دهدهي است . راحتي فوق اصولا از اين حقيقت ناشي مي شود كه تعداد مقسوم عليههاي دوازده از تعداد مقسوم عليههاي ده بيشتر ميباشد . دوازده بر يك ، دو ، سه ، چهار ، شش و دوازده بخشپذير است .
بنابراين بسياري از محاسبات دستي در سيستم دوجيني تا حدودي سادهتر از سيستم دهدهي هستند ، بعضي از كسرهاي معمولي كه در مبناي دهدهي به صورت عددهاي كسري متناوب در میآيند در مبناي دوجيني چنين نيستند . براي نمونه كسر 3/1 كه همان 12/4 ميباشد در مبناي دوجيني به صورت 0.4 است . بعضي از كسرهاي ساده در مبناي دوجيني به صورت زير مي باشند .
دوجيني 0.2 = دهدهي 12/2=6/1
دوجيني 0.3 = دهدهي 12/3=4/1
دوجيني 0.4 = دهدهي 12/4=3/1
دوجيني 0.6 = دهدهي 12/6=2/1
با وجود راحتي ، مبناي دوجيني احتمالا هرگز براي محاسبات دستي پذيرفته نخواهد شد . ولي لازم است بدانيم ، كه سيستم شمارش در عالم و هستي ما بر پايه مبناي دوجيني يا دوازدهتايي استوار گرديده است كه در مباحث بعدي به اين موضوع بسيار مهم خواهيم پرداخت . در واقع مبناي شمارش اعداد در رياضيات مختص فيزيك نيز ، سيستم دوازدهتايي يا همان سيستم شمارش دوجيني در نظر گرفته ميشود .
چنين بهنظر ميرسد ، موجودات هوشمند منجمله انسان و UFO و USO كه توانايي انجام دادن عمليات و محاسبات رياضي را دارند بهطور ذاتي از سيستمهاي شمارش بر مبناي دهتايي و دوازدهتايي بهره ميجويند . به عكسهاي زير توجه نماييد

[IMG]
[/IMG]
دو عكس فوق مربوط به دو موجود دريايي است كه در ميان گذشتگان ما به پري دريايي شهرت يافته است اما نه به آن زيبايي كه در داستانهاي كودكانه ما آمده است . همانطور كه مشخص است تعداد انگشتان آنها در دو دست ، همانند انسان ده عدد ميباشد .
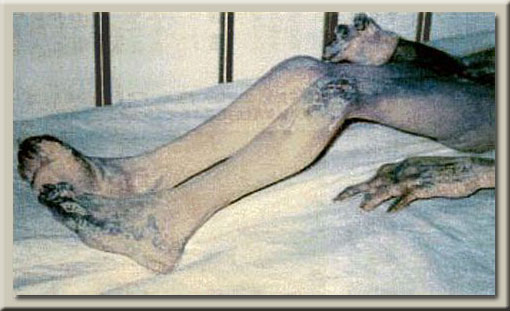
عكس فوق مربوط به جنازه يك سرنشين بشقاب پرنده است ( يوفو ) . همانطور كه مشخص است تعداد انگشتان او در دو دست ، همانند انسان 10 عدد ميباشد .

عكس فوق مربوط به ساخته دست يوفوها است . همانطور كه مشخص ميباشد تعداد انگشتان سازنده آن 12 تا بوده است كه بعضي از انسانها هم بهطور مادرزادي 12 انگشتي به دنيا ميآيند . لازم به توضيح است كه شواهد بسياري دال بر وجود رابطه نزديك مابين يوفوها و سرخ پوستان آمريكاي شمالي ، حتي فراعنه مصر در دست است و با توجه به اينكه انسانها تاكنون از سيستمهاي شمارش متعددي غير از ده استفاده نمودهاند ، پيش بيني ميشود كه موجودات باشعوري با تعداد انگشتان متفاوتي نيز وجود داشته باشند ، منجمله عكس زير .

عكسهاي زير مربوط به ترسيمهايي ميشود كه در قاره آمريكا روي زمين آنهم در ابعاد بزرگ كشف شده است و حاكي از مبناهاي متعدد اعداد رايج در ميان سرخ پوستان بوده است .


به هر حال تعداد انگشتان يك موجود هوشمند تاثير زيادي در اندوختههاي فكري و دانش او از عالم پيرامون دارد و چنين بهنظر ميرسد كه موجودات 12 انگشتي باشعورترين ، موفقترين و تكامل يافتهترين موجودات در عرصه علم و دانش منجمله رياضيات و فيزيك باشند . و مسلما موجودات باهوشتري هم يافت ميشوند كه اين سيستم شمارش اعداد را عليرغم مغايرت با تعداد انگشتان خود ، برگزيدهاند چرا كه نشانههايي از آن سيستم در ميان ما انسانها يافت ميشود كه دال بر وجود يك نوع رابطه علمي آنها با گذشتگان ما در روي سياره زمين بوده است و شايد آنگان ما نوعي همزيستي داشتهاند .
ویرایش توسط !MAHSA! : 2014/01/02 در ساعت 00:51
-
 مدیر بازنشسته
مدیر بازنشسته

دنباله اعداد طبیعی دنباله اعداد طبیعی در حالت کلی دنباله ای آشنا است.ولی بسته به این که چه نوع آرایشی از اعداد طبیعی را درنظر داشته باشیم می توان دنباله های متنوعی ایجاد کرد که همگی به نوعی معرف یک ویژگی از اعداد طبیعی هستند.
در مقالات اخیر حالتی رابررسی کردیم که در یک حالت حدی اعداد طبیعی را شامل می شد.دراین مقاله قصدداریم دنباله ای را معرفی کنیم که می تواند نواری از اعداد طبیعی را به مادهد و بدین وسیله ما می توانیم به سرعت کل دنباله را تشکیل دهیم .
به دنباله زیر توجه کنید:
N,n-1,2n-1,2n,4n-1,4n,8n-1,8n,………….. nЄIN
این دنباله دوجمله مولددارد که دوجمله اولی دنباله یعنیn و n-1 هستند.از جمله سوم به بعد دراین دنباله یک نظم خاص پدید می آید که در ذیل به آن و ویژگی هایش اشاره می شود.
دراین دنباله جملات به دودسته افراز می گردند.جملات مرتبه فرد دنباله یعنی جملات سوم وپنجم وهفتم و... وجملات مرتبه زوج یعنی جملات چهارم وششم وهشتم و...(فراموش نشود جملات اول ودوم را درنظر نگرفته ایم(جملات مولد)).
جملات مرتبه فرد از قانون زیر پیروی می کنند:
Ao=2kn-1
وجملات مرتبه زوج از قانون زیر:
AE=2kn
که در هردو قاعده k عضوی از IN است ولی تحت شرایطی که در زیر بدان اشاره می کنیم.
اگر دو جمله اول دنباله را کنار بگذاریم جملات سوم با چهارم, پنجم با ششم, هفتم با هشتم ودر کل n ام راباn+1 ام را "همسایه" می گوییم.
K برای هر همسایگی منحصر بفرد و ترتیبی است.
برای همسایگی اول k=1 و برای همسایگی دوم k=2 و برای همسایگی n ام k=n خواهد بود.
مثال)جمله دهم دنباله فوق را بیابید:
برای جمله دهم همسایگی چهارم را داریم و این جمله زوج است لذا:
A10=24n=16n
حال شرایطی را درنظر بگیرید که ما بخواهیم یک دسته اعدا طبیعی را به صورت ستون وار (نمایش ماتریسی)نشان دهیم.
بسته به این که به چند ستون ماتریسی نیاز داریم به n عدد می دهیم.n همان تعداد ستون های ماست.
درزیر نمایش ستونی برای n=5 آمده است:
5 4 3 2 1
10 9 8 7 6
15 14 13 12 11
20 19 18 17 16
25 24 23 22 21
.
.
اگر به اعداد مندرج به ستون های چهارم نگاه کنیم متوجه می شویم این اعداد همان اعداد دنباله ما هستند به ازای n=5 و جمله اول دنباله اولین مقدار ستون آخر است.
به ازای هر n ای این ماتریس را میتوان به همین ترتیب ساخت و نواره ای از اعداد طبیعی را ایجاد کرد.
سایر اعضای طبیعی نیز از روی جدول ساخته می شوند.
در این بین مهم ترین کاربرد این شیوه را می توان در "کدینگ" و "مارکینگ" اعداد نشان داد. در ضمن اگر برنامه کامپیوتری اعداد طبیعی را به کامپیوتر بدهیم و این شیوه را درخلال آن پیاده سازی کنیم پیچیدگی زمانی و مرتبه ای برنامه را می توان کاهش داد.
این نوع عدد ریزی یک ویژگی جالب دارد که در زیربدان اشاره می کنیم:
جمع درایه های متناظر در سطرهای ستون هایm ام وm-1یعنی جمع سطر های n ام ستون های m وm-1در سطر 2n ام ستون m-1 ام نمایان می شود.مثلا در مثال بالا 9در سطر2 , 19در سطر22و به همین ترتیب قرار دارد که این مساله موقعیت یابی اعداد را دراین نواره آسان تر می کند.
ویژگی های جالب تر این دنباله را وقتی متوجه می شویم که این دنباله را به صورت باینری در آوریم(باینری=دودویی).
این حالت که درزیر بدان اشاره می کنیم درتمام جدول های m*n جواب می دهد.
بایک مثال حالت مذکوررا بررسی کرده و آن راتعمیم می دهیم:
به دنباله زیر توجه کنید:
N-1,n,2n-1,2n,4n-1,4n,…
این دنباله را درازای n=5 اجرا می کنیم و جدول اعداد زیر را بدست می آوریم:
5 4 3 2 1
10 9 8 7 6
15 14 13 12 11
20 19 18 17 16
25 24 23 22 21
مطابق روش ارایه شده در ابتدای مقاله اعداد 9و19 را درنظر می گیریم:
اگر این اعداد رادر مبنای 2 تبدیل واحد کنیم داریم:
2 (1001)=9
2 (10011)=19
برای اطمینان بیشتر 39 رانیز در نظر می گیریم:
2 (100111)=39
ملاحظه می شود یک نظم و ترتیبی بین اعداد ایجاد شده در مبنای 2 دراین اعدا د وجود دارد.
دراین حالت یک پایه مبنای عملگر تعیین می کنیم و بقیه تغییر مبنا ها را براین اساس ایجاد می نماییم:
این پایه مبنا را"عملگر مخصوص" گوییم
در این حالت (حالت مثال فوق)پایه مبنا را به صورت زیر در نظر می گیریم:
( *1001)را پایه مبنا (عملگر مخصوص) این جدول در نظر می گیریم که x در ازای هر واحد که دنباله جلو می رود یک 1 اضافه می کند.
یعنی (1001)برابر 9 , (10011) برابر19 و به همین ترتیب سایر جملات دنباله به صورت باینری (دو دویی) نگاشته می شود.
در مثال های مختلف این موضوع را بهتر جلوه می دهیم:
مثال)Γ مارکینگ را برای جدول 4*5 (5 سطرو4ستون) اعداد طبیعی انجام داده و کد باینری آن را مشخص کنید:
4 3 2 1
8 7 6 5
12 11 10 9
16 15 14 13
20 19 18 17
2 (111)=7
2 (1111)=15
111x)=کد باینری مخصوص
نام این تبدیل را به خاطر نوع قرار گیری اعداد دنباله در جدول (شبیهΓ) تبدیل Γ می نامیم و به خاطر کاربردی که این سبک در عملیات کدینگ و مارکینگ اعداد دارد "Γ مارکینگ"نام گرفته است.
مثال)Γ مارکینگ را برای دنباله زیر در ازای n=3 انجام دهید و کد باینری آن را بدست آورید:
n-1,n,2n-1,2n,4n-1,4n,8n-1,8n
2 (101)=5
2 (1011)=11
2 (10111)=23
2 (101x)=کد باینری مخصوص
عکس این عمل نیز صادق است .یعنی ازروی کد مخصوص باینری می توان دنباله و در نتیجه آرایش اعداد را تعیین کرد.
درست عکس اعمال انجام شده چاره کار است.
اکتت(8 تایی)سازی مبناها در این دنباله:
در روش اکتت کردن مبناها (بردن عدد به مبنای 8) دراین نواره(دنباله)ترتیب خاص و جالبی بدست می آید.البته لازم به ذکر است که این روش زمانی عملی می شود که حداقل 5 ستون در جدول اصلی داشته باشیم.
اگر "گاما مارکینگ" را برای جدولی با حداقل 5 ستون انجام دهیم (جدول شماره 1)دنباله زیر در نواره هاپدید می آید:
n-1,n,2n-1,2n,4n-1,4n,… nЄIN
که دراین حالت N=5 خواهد بود.
اگر اعداد پدید آمده در نواره که برای ما اهمیت دارند(9و19..) را به مبنای 8 ببریم داریم:
8 (11)=9
8 (23)=19
واگر به همین ترتیب ادامه دهیم می بینیم اعدادی که از اکتت سازی n ستون بدست می آیند اعداد مبنای 10 در گاما مارکینگ n+1 ستون می باشند که این ویژگی جالب تر این روش در دنباله های سازنده این نواره ها می باشد.
با آرزوی موفقیت برای کلیه پیشگامان علم/دانشمند
-
 مدیر بازنشسته
مدیر بازنشسته

ریاضی و راز افلاطون در رساله تیمائوس به توصیف جهان طبیعی و فیزیكی می پردازد. در توصیفات افلاطون، آنچه چشمگیر است (و شاید متأثر از فیثاغوریان) میل به ریاضیاتی كردن همه چیز است، به علاوه ارسطو می گوید: افلاطون قائل به این بود كه:
▪صور، اعدادند
▪ اشیاء به سبب بهره مندی از اعداد موجودند.
▪ اعداد مركبند از واحد و «بزرگ و كوچك» و یا «دوی نامتعین» (به جای محدود و نامحدود فیثاغوری)
▪ ریاضیات وضع واسطه ای میان «صور» و اشیاء دارند.
همچنین او قائل بود كه حركات پیچ پیچ اجرام آسمانی با قانون ریاضی مطابق است و نظم در اجسام طبیعی، قابل بیان به نحو ریاضی اند. هرچند گرایش تام و تمام به ریاضی كردن همه چیز را امری ناموفق، ازسوی افلاطون دانسته اند. لكن آنچه در این كوشش برای ما، مهم است، این است كه آیا وی با عقلانی كردن واقعیت و بخصوص طبیعت محسوس، از طریق ریاضیاتی كردن آن، به سوی نوعی ماشین گرایی قدم برنمی دارد؟ عجیب می نماید كه كسی كه درباره عروج به زیبایی مطلقش تحت الهام از ارس در رساله میهمانی سخن می گوید، چنین رأیی را قائل شود. آیا باید بر آن شد كه در تمام رساله های دیگر، سقراط حقیقتاً به عنوان سقراط سخن نگفته است و اكنون در تیمائوس، افلاطون، آرای خود را بیان داشته است؟
آیا انتساب صور به اعداد آنها را از جایگاه رفیعشان به سوی یك دستگاه ماشینی تنزل نمی دهد؟
هرچند به نظر می رسد از سویی با ریاضیاتی شدن جهان طبیعی و جهان مثل و تبدیل آن به جهان قوانین معقول، افلاطون به سوی ماشینی كردن جهان پیش می رود و از سوی دیگر و در مقابل این رأی گفته شده است كه از قضا ریاضیاتی كردن طبیعت، اعتلای آن است. گاهی نیز شاهد این امر كه این اصالت ریاضیات با عروج به زیبایی مطلق ناسازگار نیست، از فیثاغوریان و گرایش همزمان آنان به ریاضیاتی كردن همه چیز و درعین حال عرفان مداری آنان سخن به میان آمده است.۱
ازسوی دیگر می دانیم كه اشكال، اعداد و اسرار مربوط بدانها نزد حكما و عرفای اسلامی جایگاهی ویژه داشته است و محاسبات، مربوط به جداول خاص علوم غریبه نیز مثالی دیگر از این امر می تواند باشد.
آیا در این گونه عقاید و آرا نیز می توان سؤال پیشین را پرسید؟ آیا اینكه اعداد، «اصل» اشیاء و موجودات، پنداشته شوند، می تواند ترس از ماشین شدن طبیعت را در دیدگاه قائلان به قول مذكور برای ما ایجاد نماید؟
پاسخ چنین پرسشی منفی به نظر می رسد. اما تفاوت چنین اصالت ریاضیاتی با اصالت ریاضیات علوم جدید (و به عنوان مثال بسیار ناب آن، اصالت ریاضیات دكارت) چیست؟
دكارت نیز قائل به اصالت ریاضی بود و می خواست كه عالم و آدم را با روابط ریاضی بسنجد و توصیف كند. او در پی تحقق یك «ریاضیات عمومی» بود كه شاید بشود تمام معرفت را با آن توصیف كرد. ۲ اوج هنر دكارت در تلاش برای تبیین ریاضیاتی از جهان را باید در هندسه تحلیلی او جست وجو كرد. هندسه تحلیلی، ابزاری است كه دكارت به وسیله آن اعداد را به جهان جسمانی نسبت می دهد. تنها با ظهور چنین ابزاری است كه ما توانایی می یابیم تا برای جهان جسمانی پیرامون خود، معادله بنویسیم. دكارت مانند فیثاغورث، هندسه را واسطه ارتباط جهان با اعداد، قرار می دهد. او در دستگاه مختصات هندسی اش، اعداد را با نقطه هایی متساوی الفاصله روی محورهای ممتد، متناظر می كند و جهان را درون این دستگاه قرار می دهد و از طریق تناظری كه برقرار می كند برای هر نقطه از عالم جسمانی، یك زوج ترتیبی از اعداد را درنظر می گیرد.
به این ترتیب، مختصات یكه ای برای هر نقطه پیدامی شود. وقتی این اختراع دكارت را در كنار رأی فلسفی اش قرار می دهیم، در می یابیم كه در نظر وی از آنجا كه جسم بودن، همان ممتدبودن است،۳ تمام جهان جسمانی، قابل تحلیل به وسیله معادلات عددی خواهد بود. ثنویت دكارتی موجب آن می شود كه وی در استفاده از این روش تحلیل جهان مادی كاملاً فارغ البال باشد و حتی در استفاده از آن در توصیف بدن انسان و حركات اجزای آن نیز تردید به خود راه ندهد. چنانكه قصد كرده بود، حركت قلب را با مبادلات گرمایی درآن توضیح دهد. ۴
در اینجا با تصویری از ماشینی كردن تام جهان روبروییم و یقیناً این از توصیف ریاضیاتی جهان به وسیله دكارت ناشی شده است. همین روند و ادامه همین تلاشها است (كما اینكه قبل از دكارت در گالیله و كپرنیك و... این روحیه حكم است) كه منجر به فیزیك نیوتنی و اكنون فیزیك جدید شده است. اما تفاوت دركجاست؟ چرا به نظر می رسد، نزد فیثاغوریان و صوفیان و حكمای متأثر از فیثاغوریان، ریاضیات نوعی آمیزش با عرفان دارد و طبیعت را بالا می برد و نزد دكارت گرایش به ریاضیات جهان را ناسوتی می كند؟ و چرا در افلاطون هردو وجه دیده می شود؟
به نظرمی رسد پاسخ این پرسشها را می بایست در مفهوم معادله جست وجو كرد. فیثاغوریان هرگز معادله ریاضی برای جهان ننوشتند. صوفیه و عرفا و حكمای بعد از آنها نیز. افلاطون نیز گویا چنین است. اما با آنها یك تفاوت كوچك دارد. او می گوید كه می توان نظم اشیاءطبیعی و نیز حركت پیچ در پیچ اجرام آسمانی را به زبان ریاضی آورد. آنچنان كه فیثاغوریان نظم مسموعات و نغمات را به زبان ریاضی برگرداندند (پس معادله نوشته اند!) و واضح است كه نگاشتن نظم طبیعت به زبان ریاضی، چیزی جز معادله نیست (هرچند در شمایل معادلات امروزی نباشد، آنچنان كه از آن دكارت نیز كاملاً امروزی نبود). معادله جهان را توصیف می كند و خبر از چگونگی عالم می دهد، اما نزد فیثاغوریان، اعداد، ماهیت موجوداتند و حقیقت آنان را بیان می كنند. آنها اعداد را «اصل» اشیاء و به طور كلی موجودات می دانستند، (افلاطون نیز تلاش داشت چنین كند) همانگونه كه متفكران ایونی پیش از آنان، آب و هوا و نامتعین و عقل را منشأ هستی شمرده بودند. با این حساب باید گفت فیثاغوریان درباره موسیقی اشتباه می كردند كه گمان می كردند ماهیت عددی آن را كشف كرده اند. (شاید ما هم در اشتباهیم كه گمان می كنیم رابطه عددی و سمعی موسیقی، تنها تناظر است!) ولی به هرطریق، شك نمی توان كرد كه برای آنها آنچه از عدد بیش از هرچیز اهمیت داشته، این بوده كه آنها چیستی موجوداتند. ولی برای دكارت اعداد، ماهیت امتداد نیستند. ما تنها اعداد را با امتداد متناظر می كنیم تا بتوانیم برای حركات و سكنات جسمانی معادله بنویسم.
افلاطون نیز، هم از چگونگی سخن گفته و هم از چیستی و می خواسته هردو را با ریاضیات پاسخ دهد. اولی به نظر ماشینی كردن جهان می رسد و دومی اعتلا دادن آن.
سخن دقیقتر در این باب را باید اینگونه بیان كرد كه همه چیز در عطف توجه به چگونگی در جهان و در آوردن آن به هیأت ریاضیات نیست كه دیدگاه طبیعیات جدید را ناسوتی كرده است. درحقیقت مسأله اصلی، تبدیل جهان و كل موجودات به واقعیت است. مراد ازواقعیت، همین جهان محسوسی است كه نزدیك دستان ماست. وقتی سؤال از ماهیت را حذف كنیم و یا پاسخ آن را به خاصیتی واقعی حواله دهیم، چنین اتفاقی می افتد. در این صورت ورای واقعیت، هیچ باطنی نخواهدبود و واقعیت، به خودی خود، قابل توصیف و تحلیل است. (این مقام از آنچه افلاطون در آن اندیشه می كرد، به كلی دور است). این مهم را دكارت از طریق حواله دادن ماهیت جسم به امری واقعی یعنی امتداد انجام داد، هرچند برخی معتقدند كه دكارت امتداد را جوهر جسم نمی دانست بلكه آن را صفت اساسی آن تصور می كرد. این درست نقطه مقابل تفكر ایونی و بخصوص فیثاغوری (و همچنین افلاطونی) است. فیثاغوریان در پشت دنیای محسوس، درپی حقیقتی بودند كه آن را در اعداد جستند.
حركت دیگری كه به این واقعی كردن جهان مدد می رسانید، واقعی كردن ازطریق مفهوم جرم بود. طرح هندسی دكارت برای توصیف عالم ناكام ماند (او در حقیقت با تصور ممتد به عنوان جسم، مكان را با جسم یكی فرض كرد و شاید این یكی از دلایلی باشد كه او تمام جهان را پرمی داند)، ۵ زیرا مفهوم حركت نیز كه او علاوه بر امتداد برای ماده فرض كرده بود هنوز كافی نبود.
سالیانی پس از دكارت، نیوتن بود كه نخست بار توانست آنچه در دل دكارت می گذشت را به واقعیت فراخواند. او برای این كار به مفهوم جرم و نیرو نیاز داشت، اما جرم را وی جوهری ورای دریافت محسوس ما اعلام نكرد، بلكه آن را برحسب كیفیات آشنای آن روزگار تبیین نمود (نخستین بار آن را برحسب چگالی و وزن بیان كرد). ۶ حتی آغاز پروژه نسبیت انیشتین را باید در شكست برنامه دكارت برای تحلیل همه چیز عالم جسمانی به امر ممتد جست وجو كرد، چه انیشتین فقط فرض كرد كه نور برای انتشارش نیاز به هیچ محیط مادی ای ندارد. ازجمله « اتر » كه دكارت، نیوتن و فیزیكدانان زمان انیشتین عدم وجود آن را اساساً نمی توانستند تصور كنند. اتر همان ماده لطیفی است كه تمام جهان را پركرده است. به این ترتیب می توان دید كه درحالی كه صوفیه، عرفا و حكما چه در قرون وسطی و چه در زمان یونان باستان در پی چیستی جهان بوده اند (ازجمله فیثاغوریان) عالمان علوم تجربی جدید پس از «رنسانس» درپی بیانی از جهان بودند كه «محاسبه پذیر» باشد.
از این جهت می توان دریافت كه تكنولوژیك بودن، ذات و فصل علوم جدید است، برخلاف آنكه گمان می رود كه «تكنولوژی» تنها كاربرد فرعی علومی است كه معطوف به حقیقتند.
منبع:
علی عبدحق
پی نوشت:
۱- تاریخ فلسفه، فردریك كاپلستون، ص۲۲۴-۲۲۸
۲- تاریخ فلسفه، فردریك كاپلستون. ج۴ صص ۹۰-۹۴
۳- همان صص ۱۵۲-۱۵۳
۴- فلسفه علم، كاپالدی، ص ۱۹۱
۵- ر. ك دكارت، تام سورل، ترجمه معصومی همدانی صص ۴۶-۵۱
۶- مبادی مابعدالطبیعی علوم برث ص ۲۳۸
روزنامه ایران
-
 مدیر بازنشسته
مدیر بازنشسته

قدرت اعداد سال ها پیش در یکی از کلاس های ریاضیات مدارس آلمان، آموزگار برای اینکه مدتی بچه ها را سرگرم کند و به کارش برسد؛ از آنها خواست تا مجموع اعداد از یک تا صد را حساب کنند. پس از چند دقیقه یکی از شاگردان کلاس گفت: مجموع این اعداد را پیدا کرده و حاصل عدد ۵۰۵۰ می شود. با شنیدن این عدد معلم با حیرت فراوان او را به پای تخته برد تا روش محاسبه خود را توضیح دهد. به نظر شما این شاگرد باهوش که بعدها یکی از بزرگ ترین و معروف ترین ریاضیدانان دنیا شد.
چه روشی را به کار بست؟ او اعداد یک تا صد را به ردیف پشت سرهم نوشت، سپس بار دیگر همین اعداد را بالعکس، این بار از صدتا یک، درست در ردیف زیرین اعداد قبلی نوشت. طوری که هر عدد زیر عدد ردیف بالاتر قرار گرفت.وی مشاهده کرد که مجموع هر کدام از ستون های به وجود آمده ۱۰۱ است. سپس نتیجه گرفت که صد تا عدد ۱۰۱ داریم که حاصل مجموع آنها می شود ۱۰۱۰۰=۱۰۱*۱۰۰. پس از آن تنها کافی بود که این مجموع به دست آمده نصف شود یعنی:
۵۰۵۰=۲/۱۰۱۰۰
شاید «شارل فردریک گاوس» شاگرد با ذکاوت کلاس که این روش جالب را به کاربرد، آن هنگام نمی دانست، روش بسیار کارا و مفیدی را برای جمع بستن رشته ای از اعداد ارائه داده است که تا سالیان سال مورد استفاده ریاضیدانان خواهد بود.اکثر مفاهیم ریاضی به قدری با زندگی روزمره ما گره خورده است که تمام مردم بدون آگاهی داشتن و واقف بودن به آن، از کنارش می گذرند و تنها کاربر خوبی هستند و بس!
حتماً تا به حال با این عبارات در رادیو، تلویزیون یا موارد مختلف دیگر برخورد کرده اید: «وزارت آب و یا وزارت نیرو اعلام کرده است که میزان پرداختی قبض ها به صورت تصاعدی بالا می رود و از مصرف کنندگان تقاضا نمود که نهایت صرفه جویی را درمصرف آن داشته باشند.» حتماً در بیشتر موارد نیز از اینکه هزینه مصرف آب یا برق شما بسیار گران شده است گله مند و شاکی بوده اید و بسیار تعجب کرده و یا شاید هم فکر کرد ه اید که اشتباهی رخ داده است!
اما در واقع این چنین نبوده است. بلکه این وزارتخانه ها و جاهای دیگر از این قبیل با به کار بردن یک مفهوم ساده ریاضی که از روابط جالب بین اعداد نشات می گیرد، تلاش نموده اند با این روش اندکی از مصرف سرانه انرژی های مفید در کشور بکاهند. بسیاری از رشته های اعداد در ریاضیات از قاعده و قانون خاصی پیروی می کنند. بدین صورت که مثلاً هر عدد نسبت به عدد قبلی خود به اندازه ثابتی کاهش یا افزایش می یابد، به این رشته از اعداد تصاعد «عددی» (حسابی) گویند.
برای مثال در رشته اعداد ۱، ۴، ۷، ۱۰، ۱۳ و ... هر عدد نسبت به عدد قبلی خود سه واحد بیشتر است. حال رشته ای از اعداد را در نظر بگیرید که در آن هر عدد نسبت به عدد ماقبل خود به اندازه توان هایی از یک عدد ثابت افزایش یا کاهش یافته باشد. به این رشته از اعداد تصاعد «هندسی» گویند.
برای مثال رشته اعداد ۱، ۲، ۴، ۸، ۱۶ و... را در نظر بگیرید. اگر کمی دقت کنید متوجه می شوید که هر عدد نسبت به عدد قبلی خود، دو برابر شده است. به عبارت دیگر در این رشته از اعداد با توان هایی از عدد ۲ و یا اعداد دیگر مواجه هستیم.
یعنی :...و۲۴، ۳ ۲، ۲ ۲۲۱۲۰،، به ترتیب از چپ به راست می شود ...و ۱۶، ۸، ۴، ۲۱،
اگر کمی حوصله کنید و با ما همراه باشید مثال ها و داستان های جالبی از خاصیت شگفت آور این رشته از اعداد خواهید خواند که حتماً متعجب می شوید.
در گذشته های دور، یکی از پادشاهان هندوستان به ازای یاد دادن سرگرمی خوبی به او، جایزه بزرگی تعیین کرد. می دانید که هندی ها در ابداع و اختراع روابط شگفت انگیز بین اعداد بسیار توانا هستند و تاریخچه بلندی در این زمینه دارند. روزی یکی از همین دانشمندان متبحر کار با اعداد، نزد پادشاه رفت و بازی شطرنج را به او آموخت. کسی چه می داند، شاید بازی شطرنج از همان زمان اختراع شده باشد.این مرد زیرک به ازای سرگرمی خوبی که به پادشاه آموخته بود از وی خواست تا به ازای ۶۴ خانه شطرنج به او گندم دهد. بدین ترتیب که از یک دانه گندم برای خانه اول آغاز کند و به هر خانه شطرنج که رسید تعداد دانه های گندم را نسبت به خانه قبل دو برابر افزایش دهد.
مثلاً برای روز چهارم پادشاه می بایست تعداد ۱۶=۲۴ دانه گندم به مرد فاضل بدهد. مرد خردمند شرط کرد که در صورت عدم توانایی پرداخت این گندم ها از سوی پادشاه می باید تاج و تخت هندوستان را برای همیشه ترک کند. پادشاه نیز با کمال میل پذیرفت و در دل به بی خردی آن ناشناس خندید. مسلماً در روزهای اول مشکلی وجود نداشت. اما مشکل اصلی از آنجا شروع می شد که این اعداد به صورت شگفت آوری بزرگ می شدند. در روز دهم تعداد ۱۰۲۴=۲۱۰ دانه گندم باید پرداخت می شد که تعداد زیادی نیست. اما روز بیستم تعداد قابل ملاحظه ای می شود یعنی ۵۷۶/۰۴۸/۱=۲۲۰ دانه گندم. فکر می کنید وقتی که به روز آخر یعنی خانه شصت و چهارم برسید چه اتفاقی بیفتد. درست حدس زده اید پادشاه ما به ....=۲۶۴ دانه گندم نیاز دارد که این تعداد گندم با تمام دانه های شن و ماسه موجود بر روی زمین برابری می کند!
در روزهای آخر این شرط تازه پادشاه هند متوجه شد که چه کلاه بزرگی سرش رفته است اما چاره ای جز کناره گیری از تاج و تخت نبود!مثال های بسیاری از این دست موجود است که به قدرت شگرف اعداد و بیشتر از آن به قدرت تفکر انسان هایی که راه سود بردن از آن را بدانند اشاره می کند.
منبع:
فریبا پایروند ثابت
مرکز ریاضیات
-
 مدیر بازنشسته
مدیر بازنشسته

یک کاغذ را چند بار می توان تا کرد؟ شاید تا کنون شده باشد که در مواقعی که بیکار هستید یا اینکه انتظار خبر مهمی را می کشید برای سرگرم کردن خودتان کاغذی را که در اطرافتان هست بردارید و شروع به تا کردن آن کنید و بعد از چند بار متوجه شوید که دیگر نمی شود کاغذ را تا کرد. در این صورت یا از تا کردن کاغذ منصرف می شوید یا آن را باز می کنید و دوباره شروع به تا کردنش می کنید... البته ممکن است قبل از اینکه به آن زمان برسید خبر مهم به شما داده شود و کاغذ را به جای اولش برگردانید !!!
این مسئله را همه ما تجربه کرده ایم اما شاید هیچ کدام از ما به طور جدی روی آن فکر نکرده باشیم.اگر ورق را هر بار طوری تا کنید که اندازه آن نصف شود بیش از ۷ یا ۸ بار نمی توانید آن را تا کنید. مهم نیست ورق اولیه شما چقدر بزرگ باشد. شاید تا به حال این قضیه را شنیده باشید و سعی کرده باشید که آن را امتحان کنید و متوجه شده باشید که تا کردن کاغذ بیش از۷ یا ۸ بار بسیار سخت است. آیا می توان گفت که این اعداد یک محدودیت مستدل و عمومی برای تا کردن کاغذ هستند؟فرض کنید شما کاغذی را انتخاب کرده اید که دارای پهنای w و ضخامت t است . اگر شما شروع به تا کردن ورق از یک سمت بکنید وقتی به جایی برسید که دیگر نتوانید کاغذ را تا کنید یک نوار باریک خواهید داشت.با هر تا کردنی ضخامت کاغذ دو برابر می شود و پهنای آن نصف خواهد شد. یعنی بعد از N بار تا کردن ضخامت خواهد بود و البته مشخص است که پهنا می شود و نسبت ضخامت به پهنا برابر می شود.اگر با کاغذی به پهنای ۱۱cm و ضخامت ۰.۰۰۲cm این کار را انجام دهید بعد از ۷ بار تا کردن نسبتt/w برابر ۱/۶ می شود. این بدان معنیست که اندازه ضخامت از پهنا بیشتر می شود و در نتیجه دیگر قادر به تا کردن کاغذ نخواهید بود. اگر این کاغذ را ۵۰ بار بزرگتر کنید شاید بتوانید آن را تا ۱۰ بار هم تا کنید.اگر به صورت متناوب کاغذ را از عرض و طول تا کنید ممکن است تعداد دفعات بیشتری بتوانید به تا کردن کاغذ ادامه دهید. در این صورت هر بارضخامت دو برابر می شود در صورتی که پهنا هر دو دفعه یک بار نصف می شود.چندین سال پیش هنگامی که بریتنی گالیوان در دبیرستان درس می خواند با این مسئله رو به رو شد که چگونه کاغذی زا ۱۲ بار تا کند . او باید برای گرفتن نمره از یکی از کلاسهایش این مسئله را حل می کرد. بعد از آزمایش راه های مختلف او موفق شد که ورقه نازکی از طلا را ۱۲ بار تا کند. اما مسئله طرح شده در باره کاغذ بود و نه طلا.گالیوان بر روی معادله تعداد دفعاتی که می توان یک کاغذ با اندازه معین را تا کرد کار کرد.
که در آن L کمترین درازای کاغذ، t میزان ضخامت کاغذ و n تعداد دفعاتی است که می توان کاغذ را تا کرد. واحد t و L باید یکسان باشد.
برای یک طول و ضخامت معین عبارت بیانگر آن است که صفحه بعد از n بار تاکردن چند برابر کوچک شده است. با n=۰ شروع می کنیم و به همین ترتیب به رشته ای از اعداد به این صورت می رسیم:
۰, ۱, ۴, ۱۴, ۵۰, ۱۸۶, ۷۱۴, ۲۷۹۴, ۱۱۰۵۰, ۴۳۹۴۶, ۱۷۵۲۷۴, ۷۰۰۰۷۴, ۲۷۹۸۲۵۰, . . .
این به این معنی است که در تای دوازدهم ۲۷۹۸۲۵۰ برابر مقدار کاغذی که در تای اول از دست می رود از دست خواهد رفت.گالیوان در کتابی با نام Historical Society of Pomona Valley چگونگی به دست آوردن این معادله و تلاشش برای حل مشکل را توضیح داده است. بالاخره در June ۲۰۰۲ گالیوان یک کاغذ بزرگ را ۱۲ بار تا کرد.
-
 مدیر بازنشسته
مدیر بازنشسته

نكات آمار و احتمال آمار رشته وسیعی از ریاضی است كه راههای جمع آوری، خلاصه سازی و نتیجه گیری از داده ها را مطالعه می كند. این علم برای طیف وسیعی از علوم دانشگاهی از فیزیك و علوم اجتماعی گرفته تا انسان شناسی و همچنین تجارت، حكومت داری و صنعت كاربرد دارد.
هنگامی كه داده ها جمع آوری شدند چه از طریق یك شیوه نمونه گیری خاص یا به وسیله ثبت پاسخ ها در قبال رفتارها در یك مجموعه آزمایشی ( طرح آزمایشcf ) یا به وسیله مشاهده مكرر یك فرایند در طی زمان ( سری های زمانی ) خلاصه های گرافیكی یا عددی را می توان با استفاده از آمار توصیفی به دست آورد.
الگوهای موجه در داده ها سازمان بندی می شوند تا استنباط در مورد جمعیت های بزرگتر به دست آید كه این كار با استفاده از آمار استنباطی صورت می گیرد و تصادفی بودن و عدم حتمیت در مشاهدات را شناسایی می كند. این استنباط ها ممكن است به شكل جوابهای بله یا خیر به سؤالات باشد ( آزمون فرض )، مشخصه های عددی را برآورد كند ( تخمین ) ، پیش گویی مشاهدات آتی باشد، توصیف پیوند ها باشد ( همبستگی ) ویا مدل سازی روابط باشد ( رگرسیون ).
شبكه توصیف شده در بالا گاهی اوقات به عنوان آمار كاربردی اطلاق می شود. در مقابل، آمار ریاضی ( یا ساده تر نظریه آماری ) زیر رشته ای از ریاضی كاربردی است كه از تحلیل و نظریه احتمال برای به كارگیری آمار برروی یك پایه نظری محكم استفاده می كند.
● احتمال
كلمه احتمال از كلمه لاتین probare ( به معنی اثبات یا آزمایش كردن ) منشأ می گیرد. در زبان محاوره، احتمال یكی از چندین لغتی است كه برای دانسته یا پیشامدهای غیر حتمی به كار میرود و كم و بیش با لغاتی مثل مشابه، با ریسك، خطرناك، نامطمئن، مشكوك و بسته به متن قابل معاوضه می باشد. شانس، بخت و شرط بندی از لغات دیگری هستند كه نشان دهنده برداشت های مشابهی هستند. همانگونه كه نظریه مكانیك تعاریف دقیقی از عبارات متداولی مثل كار و نیرو دارد، نظریه احتمال نیز تلاش دارد تا برداشت های احتمال را كمیت سازی كند.
● روش های آماری
۱) مطالعات تجربی و مشاهداتی
ـ هدف كلی برای یك پروژه تحقیقی آماری، بررسی حوادث اتفاقی بوده و به ویژه نتیجه گیری روی تأثیر تغییرات در مقادیر شاخص ها یا متغیر های مستقل روی یك پاسخ یا متغیر وابسته است. دو شیوه اصلی از مطالعات آماری تصادفی وجود دارد : مطالعات تجربی و مطالعات مشاهداتی . در هر دو نوع از این مطالعات، اثر تغییرات در یك یا چند متغیر مستقل روی رفتار متغیر های وابسته مشاهده می شود. اختلاف بین این دو شیوه درچگونگی مطالعه ای است كه عملاً هدایت می شود.
ـ یك مطالعه تجربی در بردارنده روش های اندازه گیری سیستم تحت مطالعه است كه سیستم را تغییر می دهد و سپس با استفاده از روش مشابه اندازه گیری های اضافی انجام می دهد تا مشخص سازد كه آیا تغییرات انجام شده، مقادیر شاخص ها را تغییر می دهد یا خیر. در مقابل یك مطالعه مشاهداتی، مداخلات تجربی را در بر نمی گیرد. در عوض داده ها جمع آوری می شوند و روابط بین پیش بینی ها و پاسخ بررسی می شوند.
ـ یك نمونه از مطالعه تجربی، مطالعات Hawthorne مشهور است كه تلاش كرد تا تغییرات در محیط كار را در كمپانی الكتریك غربی Howthorne بیازماید. محققان علاقه مند بودند كه آیا افزایش نور می تواند كارایی را در كارگران خط تولید افزایش دهد. محققان ابتدا كارایی را در كارخانه اندازه گیری كردند و سپس میزان نور را در یك قسمت از كارخانه تغییر دادند تا مشاهده كنند كه آیا تغییر در نور می تواند كارایی را تغییر دهد. به واسطه خطا در اقدامات تجربی، به ویژه فقدان یك گروه كنترل، محققان در حالی كه قادر نبودند آنچه را كه طراحی كرده بودند، انجام دهند توانستند كه محیط را با شیوه Hawthorne آماده سازند.
ـ یك نمونه از مطالعه مشاهداتی، مطالعه ایست كه رابطه بین سیگار كشیدن و سرطان ریه را بررسی می كند. این نوع از مطالعه به طور اختصاصی از یك آمار گیری ( پیمایش ) استفاده می كند تا مشاهدات مورد علاقه را جمع آوری كند و سپس تجزیه و تحلیل آماری انجام دهد. در این مورد، محققان مشاهدات افراد سیگاری و غیر سیگاری را جمع آوری می كنند و سپس به تعداد موارد سرطان ریه در هر دو گروه توجه می كنند.
مراحل پایه برای انجام یك تجربه عبارتند از :
ـ برنامه ریزی تحقیق شامل تعیین منابع اطلاعاتی، انتخاب موضوع تحقیق و ملاحظات اخلاقی برای تحقیق و روش پیشنهادی.
ـ طراحی آزمون شامل تمركز روی مدل سیستم و اثر متقابل متغیر های مستقل و وابسته.
ـ خلاصه سازی از مجموعه مشاهدات برای جامعیت بخشیدن به آنها با حذف جزئیات ( آمار توصیفی ).
ـ رسیدن به اجماع در مورد آنچه مشاهدات درباره دنیایی كه مشاهده می كنیم به ما می گویند ( استنباط آماری ).
ـ ثبت و ارائه نتایج مطالعه.
۲) سطوح اندازه گیری
چهار نوع یا مقیاس اندازه گیری در آمار استفاده می شود. چــهار نوع یا سطح اندازه گیری ( ترتیبی، اسمی، بازه ای و نسبی ) دارای درجات متفاوتی از سودمندی در تحقیقات آماری دارند. اندازه گیری نسبی در حالی كه هم یك مقدار صفر و فاصله بین اندازه های متفاوت تعریف می شود بیشترین انعطاف پذیری را در بین روش های آماری دارد كه می تواند برای تحلیل داده ها استفاده شود. مقیاس تناوبی با داشتن فواصل معنی دار بین اندازه ها اما بدون داشتن میزان صفر معنی دار ( مثل اندازه گیری IQ یا اندازه گیری درجه حرارت در مقیاس سلسیوس ) در تحقیقات آماری استفاده می شود.
۳) تكنیك های آماری
بعضی از آزمون ها و روش های آماری برای مشاهدات تحقیقی آماری شناخته شده عبارتند از :
▪ آزمون تی استیودنت
▪ آزمون توان دوم كای ( خی دو )
▪ آنالیز واریانس ( ANOVA)
▪ آزمون Mann-Whitney U
▪ تحلیل رگرسیون
▪ همبستگی
▪ آزمون كمترین تفاوت معنی دار ( LSD ) فیشر
▪ ضریب همبستگی حاصل ضرب گشتاوری پیرسون
▪ ضریب همبستگی رتبه ای اسپیرمن
نظریه عمومی احتمال به دو اصل وابسته تقسیم می شود :
▪ احتمال كتّره ای : كه نشان دهنده احتمال پیشامدهای آینده است كه به وسیله بعضی از پدیده های فیزیكی تصادفی هدایت می شود. این اصل را می توان به پدیده های فیزیكی كه با اطلاعات كافی اصولاً قابل پیش بینی اند و پدیده هایی كه اساساً قابل پیش بینی نیستند تقسیم بندی كرد. نمونه هایی از نوع اول شامل پرتاب تاس یا بازی رولت در قمار است و یك مثال از نوع دوم از بین رفتن ماده رادیو اكتیویته است.
▪ احتمال شناختیك : كه نشان دهنده عدم قاطعیت ما در مورد گزاره ای است وقتی كه فرد آگاهی كامل از شرایط اتفاقی ندارد. چنین گزاره هایی ممكن است در مورد پیشامدهای گذشته یا آینده باشد اما نیاز به آن نیست. بعضی مثال ها از احتمال شناختیك آنهایی هستند كه در آن ها یك احتمال به گزاره ای داده می شود كه در آن یك قانون پیشنهادی فیزیك به وقوع پیوسته است و تعیین اینكه چقدر احتمال است كه یك مظنون بر اساس شواهد موجود مرتكب جنایت شده باشد.
یك سؤال كلی وجود دارد كه آیا احتمال كتره ای به واسطه عدم توانایی ما در پیش بینی دقیق نیروهایی كه ممكن است وقوع مرگ را متأثر سازند به احتمال شناختیك تبدیل شود یا اینكه چنین عدم اطمینانی در ماهیت خود واقعیت وجود دارد به ویژه در پدیده های كوانتومی كه توسط اصل عدم حتمیت هایزنبرگ بیان شده است.هرچند قوانین ریاضی مشابهی صرفنظر از تفسیر انتخاب شده اعمال می شوند، گزینه انتخابی از نظر احتمال مورد استفاده دارای معانی مهمی است كه برای مدل سازی دنیای واقعی به كار می رود.
● فرموله سازی احتمال
مانند سایر نظریه ها، نظریه احتمال نمادی از اصول احتمال در عبارات رسمی - عباراتی كه جدا از معنیشان كاربرد داشته باشند – است. این عبارات رسمی به واسطه قوانین ریاضی و منطق متأثر می شوند و هر نتیجه ای از آن بر اساس دامنه مسئله تفسیر و برداشت می شود.
حداقل دو تلاش موفق برای فرموله كردن احتمال انجام شده است كه به نام فرمول بندی كلموگروف و كاكس نامیده می شوند. در فرمول بندی كلموگروف، مجموعه ها به صورت پیشامدها و احتمال خود به عنوان معیاری روی یك سری از مجموعه ها تفسیر می شود. در فرمول بندی كاكس، احتمال به عنوان یك مقدمه اولیه قلمداد می شود ( به این معنی كه بعداً آنالیز نمی شود ) و تأكید بر روی ساخت یك رابطه سازگار از مقادیر احتمال برای گزاره ها می باشد.
در هر دو مورد، قوانین احتمال مشابه هستند به جز در مورد جزئیات عملی :
▪ احتمال عددی بین 0 و 1 می باشد.
▪ مجموع احتمال یك پیشامد یا گزاره و مكمل آن برابر 1 است؛ و
▪ احتمال مشترك دو پیشامد یا گزاره برابر با حاصل ضرب احتمال یكی از آن ها و احتمال دومی است به شرطی كه اولی رخ دهد.
● نمایش و تفسیر مقادیر احتمال
احتمال یك پیشامد عموماً به صورت یك عدد حقیقی بین 0 و 1 نمایش داده می شود. یك پیشامد غیر محتمل دارای یك احتمال دقیقاً 0 و یك پیشامد حتمی دارای یك احتمال 1 است، اما عكس آن همیشه صادق نیست؛ پیشامدهای با احتمال 0 همیشه غیر ممكن نیستند و همچنین پیشامدهای با احتمال 1 همیشه واقعیت نمی پذیرند.
اغلب احتمالاتی كه عملاً رخ می دهند اعدادی بین 0 و 1 هستند كه نشان دهنده موقعیت پیشامد روی پیوستگی بین غیر ممكن و حتمیت است. هر چه احتمال پیشامد به 1 نزدیكتر باشد، احتمال وقوع آن بیشتر است.
مثلاً اگر احتمال وقوع دو پیشامد متقابلاً ناسازگار یكسان تصور شود مثل رو یا پشت در پرتاب سكه، ما می توانیم احتمال هر پیشامد را به صورت 1 از 2 یا %50 یا ½ نمایش دهیم.
احتمالات مشابهاً به صورت بخت ها هم نمایش داده می شوند كه نسبت احتمال یك پیشامد به احتمال سایر پیشامدهاست. بخت رو شدن در پرتاب سكه (1/2)/(1 - 1/2) است كه مساوی با 1/1 است كه به صورت بخت 1 به 1 نمایش داده می شود و اغلب به صورت 1:1 نوشته می شود.
بخت های a:b برای یك پیشامد معادل با احتمال a/(a+b) است. مثلاً بخت 1:1 معادل با احتمال ½ است و نمایش 3:2 معادل با احتمال 3/5 است.
این سؤال عملاً باقی می ماند كه از احتمال چه انتظاری می توان داشت و چگونه از اعداد و ارقام می توان استفاده كرد. این سؤال همان تفاسیر و برداشت های از احتمال است. افرادی هستند كه مدعیند احتمال را می توان بر هر نوع از گزاره های منطقی غیر حتمی به كار برد كه همان استنباط بیزی است. در مقابل، افرادی هستند كه با این ایده توافق دارند كه احتمال برای پیشامدهای تصادفی همانند برآمد بعضی آزمایش های تصادفی خاص كاربرد دارد؛ به عنوان مثال نمونه گیری از یك جمعیت كه این تفسیر فراوانی گراست. چندین تفسیر دیگر نیز وجود دارد كه فرم اصلاح شده ای از یكی از این دو تفسیر هستند و در حال حاضر از مقبولیت كمتری برخوردار هستند.
● توزیع ها
توزیع احتمال، تابعی است كه احتمال را به پیشامدها یا گزاره ها تخصیص می دهد. برای هر مجموعه از پیشامدها یا گزاره ها راه های مختلفی برای تخصیص احتمالات وجود دارد به طوری كه شانس یك توزیع یا دیگری معادل با داشتن تصورات متفاوت درباره پیشامدها یا گزاره های مورد سؤال می باشد.
راه های گوناگون معادلی برای نمایش توزیع احتمال وجود دارد. شاید متداولترین آن ها تابع چگالی احتمال باشد؛ به این معنی كه احتمال پیشامد یا گزاره به وسیله انتگرال تابع چگالی به دست می آید. تابع توزیع را می توان همچنین مستقیماً نمایش داد. از یك بعد، تابع توزیع، تابع توزیع تجمعی نامیده می شود. توزیع های احتمال را می توان از طریق گشتاورها یا تابع مشخصه یا به روش های دیگر نیز نمایش داد.
یك توزیع، توزیع گسسته نامیده می شود اگر آن روی یك مجموعه گسسته شمارش پذیر مثل زیر مجموعه ای از اعداد صحیح تعریف شود. یك توزیع، توزیع پیوسته نامیده می شود اگر دارای یك تابع توزیع پیوسته باشد مثل تابع چند جمله ای یا تابع نمایی. اغلب توزیع های با اهمیت كاربردی از نوع گسسته یا پیوسته هستند اما نمونه هایی از توزیع ها هستند كه شامل هیچكدام از اینها نمی شوند.
توزیع های مهم گسسته شامل توزیع گسسته یكنواخت، توزیع پواسون، توزیع دو جمله ای، توزیع دو جمله ای منفی و توزیع ماكسول-بولتزمن می باشند.
توزیع های مهم پیوسته شامل توزیع نرمال، توزیع گاما، توزیع تی استیودنت و توزیع نمایی هستند.
▪ احتمال در ریاضیات
اصول موضوع احتمال، اساس نظریه احتمال ریاضیات را تشكیل می دهند. محاسبه احتمالات را اغلب می توان با استفاده از تركیبات یا مستقیماً با كاربرد اصول موضوع تعیین كرد.كاربردهای احتمال حتی بیشتر از آمار است كه معمولاً بر روی ایده توزیع های احتمال و قضیه حد مركزی پایه ریزی شده است.
برای به دست آوردن یك مفهوم ریاضی از احتمال، پرتاب یك سكه را در نظر بگیرید. بدیهی است كه احتمال آن كه در هر پرتاب سكه رو بیاید %50 است اما این وضعیت به تنهایی فاقد صلابت ریاضی است؛ به این معنی كه ما باید چنین انتظار داشته باشیم كه با پرتاب 10 بار سكه 5 رو و 5 پشت به دست آید اما هیچ تضمینی كه این رخ دهد وجود ندارد. برای مثال این احتمال است كه پشت سر هم 10 بار رو بیاید. پس مفهوم %50 در این متن چیست ؟
یك راه، استفاده از قانون اعداد بزرگ است. در این مورد، ما تصور می كنیم كه می توانیم هر تعداد پرتاب سكه را انجام دهیم و هر پرتاب سكه مستقل است یعنی كه برآمد هر پرتاب سكه به وسیله پرتاب قبلی تحت تأثیر قرار ندارد. اما ما N مرتبه پرتاب سكه داشته باشیم و اگر Nн تعداد مرتبه هایی باشد كه رو بیاید پس ما می توانیم برای هر N نسبت Nн/N را در نظر بگیریم.
هر قدر N بزرگ و بزرگ تر شود، ما انتظار داریم كه نسبت Nн/N به ½ نزدیك و نزدیك تر شود. این به ما اجازه می دهد كه احتمال Pr(H)
رو های سكه را به صورت حد ( ریاضی ) تعریف كنیم، هنگامی كه N به سمت بی نهایت میل میكند :
البته در كاربرد عملی، ما نمی توانیم یك سكه را به تعداد بی نهایت پرتاب كنیم بنابراین عملاً این فرمول باید در موقعیت هایی به كار گرفته شود كه در آن ها از قبل یك احتمال اولیه ای برای یك برآمد خاص تعیین كرده ایم ( در این مورد فرض ما این است كه سكه سالم است ). قانون اعداد بزرگ به ما می گوید كه Pr(H) داده شده و یا به ازای هر عدد كوچـك اختیاری є، عدد n ای وجود دارد كه برای تمام N > nداریم :
به عبارت دیگر، منظور ما از گفتن « احتمال رو ها ½ است » این است كه اگر ما سكه را به اندازه كافی پرتاب كنیم نهایتاً تعداد رو ها نسبت به تعداد كل پرتاب به ½ نزدیك می شود و سپس به هر اندازه كه تعداد بیشتری پرتاب انجام دهیم ما به ½ نزدیك تر می شویم.
توجه كنید كه یك تعریف كامل، مستلزم نظریه اندازه است كه قادر به حذف مواردی است كه مقادیر بالاتر از محدوده جواب درست نمی دهند یا حتی با نمایش مواردی كه دارای میزان صفر هستند نیز محدود نشده است.
جنبه اولیه این روش كاربرد احتمال، گاهی در هنگام مواجهه با موقعیت های دنیای واقعی با مشكل روبه رو می شود. برای مثال اگر شما یك سكه را پرتاب كنید و پشت سر هم رو بیاید برای صد مرتبه شما نمی توانید تصمیم بگیرید كه آیا این تنها یك پیشامد تصادفی محض است اگر چه ممكن است ( هرچند بعید ) كه یك سكه سالم این نتیجه را بدهد یا اینكه تصور شما این خواهد بود كه سكه سالم دچار اشكال می باشد.
▪ نكات قابل توجه در محاسبات احتمال
سختی محاسبات احتمال در تعیین تعداد پیشامدهای ممكن، شمارش رخدادهای هر پیشامد و شمارش تعداد كل پیشامدهای ممكن است. اشكال خاص در به دست آوردن نتایج معنی دار از احتمالات محاسبه شده است. یك معمای سرگرم كننده احتمال به نام مسئله Monty Hall به زیبایی چالش های موجود را نشان می دهد.
▪ كاربرد های نظریه احتمال در زندگی روزمره
یك تأثیر مهم نظریه احتمال در زندگی روزمره در ارزیابی ریسك پذیری و در تجارت در مورد خرید و فروش اجناس می باشد. حكومت ها به طور خاص روشهای احتمال را در تنظیم جوامع اعمال می كنند كه به عنوان « آنالیز خط مشی » نامیده می شود و غالباً سطح رفاه را با استفاده از متدهایی كه در طبیعت تصادفیند اندازه می گیرند و برنامه هایی را انتخاب می كنند تا اثر احتمال آن ها را روی جمعیت به صورت كلی از نظر آماری ارزیابی كنند. این گفته صحیح نیست كه آمار، خود در مدل سازی درگیر هست زیرا كه ارزیابی های میزان ریسك وابسته به زمان هستند و بنابراین مستلزم مـدل های احتمال قوی تر هستند؛ مثلاً « احتمال9/11 دیگری »؛ قانون اعداد كوچك در جنین مواردی اعمال می شود و برداشت اثر چنین انتخاب هایی است كه روش های آماری را به صورت یك موضوع سیاسی در می آورد.
یك مثال خوب اثر احتمال قلمداد شده از مجادلات خاورمیانه بر روی قیمت نفت است كه دارای اثرات متلاطمی از لحظ آماری روی اقتصاد كلی دارد. یك ارزیابی توسط یك واحد تجاری در مورد این كه احتمال وقوع یك جنگ زیاد است یا كم باعث نوسان قیمت ها می شود و سایر تجار را برای انجام كار مشابه تشویق می كند. مطابق با این اصل، احتمالات به طور مستقل ارزیابی نمی شوند و ضرورتاً به طور منطقی برخورد صورت نمی گیرد. نظریه اعتبارات رفتاری، به وجود آمده است تا اثر این تفكرات گروهی را روی قیمت ها، سیاست ها و روی صلح و مجادله توضیح دهد.
به طور استدلالی می توان گفت كه كشف روش های جدی برای ارزیابی و تركیب ارزیابی های احتمالی دارای اثر شدیدی روی جامعه مدرن داشته است. یك مثال خوب كاربرد نظریه بازی ها كه به طور بنیادین بر پایه احتمال ریخته شده است در مورد جنگ سرد و دكترین انهدام با اطمینان بخشی متقابل است. مشابهاً ممكن است برای اغلب شهروندان دارای اهمیت باشد كه بفهمند چگونه بخت ها و ارزیابی های احتمال صورت می گیرد و چگونه آن ها می توانند در تصمیم گیری ها به ویژه در زمینه دموكراسی دخالت كنند.
كاربرد مهم دیگر نظریه احتمال در زندگی روزمره، اعتبار است. اغلب تولیدات مصرفی مثل اتومبیل و وسایل الكترونیكی در طراحی آن ها از نظریه اعتبار استفاده می شود به نحوی كه احتمال نقص آن ها كاهش یابد. احتمال نقص با مدت ضمانت فرآورده معمولاً ارتباط نزدیك دارد.
● رشته های اختصاصی
بعضی علوم آن چنان به طور وسیع از آمار كاربردی استفاده می كنند كه برای خود دارای اصطلاحات خاص شده اند. این رشته ها عبارتند از :
▪ زیست آمار
▪ آمار بازرگانی
▪ داده كاوی ( كاربرد آمار و شناسایی الگوها برای كشف علم از داده ها )
▪ آمار اقتصادی ( اقتصاد سنجی )
▪ آمار مهندسی
▪ فیزیك آماری
▪ جمعیت شناسی
▪ آمار روان شناسی
▪ آمار اجتماعی ( برای تمام علوم اجتماعی )
▪ سواد آموزی آماری
▪ آنالیز فرایند و شیمی سنجی ( برای تحلیل داده ها از شیمی تحلیلی و مهندسی شیمی)
▪ مهندسی اعتبار
▪ آمار در ورزش های گوناگون به ویژه بیسبال و كریكت
آمار یك ابزار پایه ای كلیدی در تجارت و تولید است و برای درك تغییر پذیری سیستم های اندازه گیری، فرایند های كنترل ( مثلاً در كنترل آماری فرایند یا SPC )، برای خلاصه سازی داده ها و برای ساخت تصمیمات بر اساس داده ها مورد استفاده قرار می گیرد. در این نقش ها به آمار یك ابزار كلیدی و شاید تنها ابزار مورد اعتماد باشد.
● نرم افزار
▪ آمار مدرن برای انجام بعضی از محاسبات خیلی پیچیده و بزرگ به وسیله كامپیوترها استفاده می شود.
▪ تمامی شاخه های آمار با استفاده از محاسبات كامپیوتری انجام پذیر شده اند، به عنوان مثال شبكه های عصبی.
▪ انقلاب كامپیوتری با یك توجه نو به آمار « آزمایشی » و « تجربی » رویكردهایی برای آینده آمار داشته است .
شبیه سازی نسخه ای از بعضی وسایل واقعی یا موقعیت های كاری است. شبیه سازی تلاش دارد تا بعضی جنبه های رفتاری یك سیستم فیزیكی یا انتزاعی را به وسیله رفتار سیستم دیگری نمایش دهد.
شبیه سازی در بسیاری از متون شامل مدل سازی سیستم های طبیعی و سیستم های انسانی استفاده می شود. برای به دست آوردن بینش به كاركرد این سیستم ها و همچنین در تكنولوژی و مهندسی ایمنی كه هدف، آزمون بعضی سناریوهای عملی در دنیای واقعی است از شبیه سازی استفاده می شود. در شبیه سازی با استفاده از یك شبیه ساز یا وسیله دیگری در یك موقعیت ساختگی می توان اثرات واقعی بعضی شرایط احتمالی را بازسازی كرد.
▪ شبیه سازی فیزیكی و متقابل
ـ شبیه سازی فیزیكی ، به شبیه سازی اطلاق می شود كه در آن اشیای فیزیكی به جای شی حقیقی جایگزین می شوند و این اجسام فیزیكی اغلب به این خاطر استفاده می شوند كه كوچكتر یا ارزان تر از شی یا سیستم واقعی هستند.
ـ شبیه سازی متقابل كه شكل خاصی از شبیه سازی فیزیكی است و غالباً به انسان در شبیه سازی های حلقه ای اطلاق می شود یعنی شبیه سازی های فیزیكی كه شامل انسان می شوند مثل مدل استفاده شده در شبیه ساز پرواز.
▪ شبیه سازی در آموزش
شبیه سازی اغلب در آموزش پرسنل شهری و نظامی استفاده می شود و معمولاً هنگامی رخ می دهد كه استفاده از تجهیزات در دنیای واقعی از لحاظ هزینه كمرشكن یا بسیار خطرناك است تا بتوان به كارآموزان اجازه استفاده از آن ها را داد . در چنین موقعیت هایی كارآموزان وقت خود را با آموزش دروس ارزشمند در یك محیط مجازی « ایمن » می گذرانند. غالباً این اطمینان وجود دارد تا اجازه خطا را به كارآموزان در طی آموزش داد تا ارزیابی سیستم ایمنی– بحران صورت گیرد.
شبیه سازی های آموزشی به طور خاص در یكی از چهار گروه زیر قرار می گیرند :
ـ شبیه سازی زنده ( جایی كه افراد حقیقی از تجهیزات شبیه سازی شده ( یا آدمك ) در دنیای واقعی استفاده می كنند. )
ـ شبیه سازی مجازی ( جایی كه افراد حقیقی از تجهیزات شبیه سازی شده در دنیای شبیه سازی شده ( یا محیط مجازی ) استفاده می كنند. ) یا
ـ شبیه سازی ساختاری ( جایی كه افراد شبیه سازی شده از تجهیزات شبیه سازی شده در یك محیط شبیه سازی شده استفاده می كنند. ) شبیه سازی ساختاری اغلب به عنوان بازی جنگی نامیده می شود زیرا كه شباهتهایی با بازی های جنگی رومیزی دارد كه در آن ها بازیكنان، ارتش سربازان و تجهیزات را اطراف یك میز هدایت می كنند .
ـ شبیه سازی ایفای نقش ( جایی كه افراد حقیقی نقش یك شخصیت با كاری مجازی را بازی می كنند. )
▪ شبیه ساز های پزشكی
شبیه ساز های پزشكی به طور فزاینده ای در حال توسعه و كاربرد هستند تا روشهای درمانی و تشخیص و همچنین اصول پزشكی و تصمیم گیری به پرسنل بهداشتی آموزش داده شو د. طیف شبیه ساز ها برای آموزش روش ها از پایه مثل خونگیری تا جراحی لاپاراسكوپی و مراقبت از بیمار دچار ضربه، وسیع و گسترده است. بسیاری از شبیه ساز های پزشكی دارای یك كامپیوتر می باشند كه به یك ماكت پلاستیكی با آناتومی مشابه واقعی متصل است. در سایر آنها، ترسیم های كامپیوتری، تمام اجزای قابل رؤیت را به دست می دهد و با دستكاری در دستگاه می توان جنبه های شبیه سازی شده كار ر ا تولید كرد. بعضی از این دستگاه ها دارای شبیه سازهای گرافیكی كامپیوتری برای تصویر برداری هستند مثل اشعه ایكس یا سایر تصاویر پزشكی. بعضی از شبیه سازهای بیمار، دارای یك مانكن انسان نما هستند كه به داروهای تزریق شده واكنش می دهد و می توان آن را برای خلق صحنه های مشابه اورژانس های خطرناك برنامه ریزی كرد. بعضی از شبیه ساز های پزشكی از طریق شبكه اینترنت قابل گسترش می باشند و با استفاده از جستجوگرهای استاندارد شبكه به تغییرات جواب می دهند. در حال حاضر، شبیه سازی ها به موارد غربال گری پایه محدود شده اند به نحوی كه استفاده كنندگان از طریق وسایل امتیازدهی استاندارد با شبیه سازی در ارتباط هستند.
▪ شبیه ساز های پرواز
یك شبیه ساز پرواز برای آموزش خلبانان روی زمین مورد استفاده قرار می گیرد. در این شبیه سازی، به خلبان اجازه داده می شود تا به هواپیمای شبیه سازی شده اش آسیب برساند بدون آن كه خود دچار آسیب شود. شبیه سازهای پرواز اغلب برای آموزش خلبانان استفاه می شوند تا هواپیما را در موقعیت های بسیار خطرناك مثل زمین نشستن بدون داشتن موتور یا نقص كامل الكتریكی یا هیدرولیكی هدایت كنند. پیشرفته ترین شبیه سازها دارای سیستم بصری با كیفیت بالا و سیستم حركت هیدرولیك هستند. كار با شبیه ساز به طور معمول نسبت به هواپیمای واقعی ارزان تر است.
▪ شبیه سازی و بازی ها
بسیاری از بازی های ویدئویی نیز شبیه ساز هستند كه به طور ارزان تر آماده سازی شده اند. بعضی اوقات از این ها به عنوان بازیهای شبیه سازی ( sim ) نامبرده می شود. چنین بازیهایی جنبه های گوناگون واقعی را شبیه سازی می كنند از اقتصاد گرفته تا وسایل هوانوردی مثل شبیه سازهای پرواز.
▪ شبیه سازی مهندسی
شبیه سازی یك مشخصه مهم در سیستم های مهندسی است. به عنوان مثال در مهندسی برق، از خطوط تأخیری استفاده می شود تا تأخیر تشدید شده و شیفت فاز ناشی از خط انتقال واقعی را شبیه سازی كنند. مشابهاً، از بارهای ظاهری می توان برای شبیه سازی مقاومت بدون شبیه سازی تشدید استفاده كرد و از این حالت در مواقعی استفاده می شود كه تشدید ناخواسته باشد. یك شبیه ساز ممكن است تنها چند تا از توابع و عملكرد های واحد را شبیه سازی كند كه در مقابل با عملی است كه تقلید نامیده می شود.
اغلب شبیه سازی های مهندسی مستلزم مدل سازی ریاضی و بررسی های رایانه یار هستند. به هر حال موارد زیادی وجود دارد كه مدل سازی ریاضی قابل اعتماد نمی باشد. شبیه سازی مشكلات مكانیك سیالات اغلب مستلزم شبیه سازی های ریاضی و نیز فیزیكی است. در این موارد، مدل های فیزیكی نیاز به شبیه سازی دینامیك دارند.
▪ شبیه سازی كامپیوتری
شبیه سازی رایانه ای ، جزو مفیدی برای مدل سازی بسیاری از سیستم های طبیعی در فیزیك، شیمی و زیست شناسی و نیز برای سیستم های انسانی در اقتصاد و علوم اجتماعی ( جامعه شناسی محاسباتی ) و همچنین در مهندسی برای به دست آوردن بینش نسبت به عمل این سیستم ها شده است. یك نمونه خوب از سودمندی استفاده از رایانه ها در شبیه سازی را می توان در حیطه شبیه سازی ترافیك شبكه یافت. در چنین شبیه سازی هایی رفتار مدل هر شبیه سازی را مطابق با مجموعه پارامترهای اولیه منظور شده برای محیط تغییر خواهد داد. شبیه سازی های رایانه ای اغلب به این منظور به كار گرفته می شوند تا انسان از شبیه سازی های حلقه ای در امان باشد.
به طور سنتی، مدل برداری رسمی سیستم ها از طریق یك مدل ریاضی بوده است به نحوی كه تلاش در جهت یافتن راه حل تحلیلی برای مشكلات بوده است كه پیش بینی رفتار سیستم را با استفاده از یك سری پارامترها و شرایط اولیه ممكن ساخته است. شبیه سازی رایانه ای اغلب به عنوان یك ضمیمه یا جانشین برای سیستم های مدل سازی می باشد كه در آن ها راه حل های تحلیلی بسته ساده ممكن نمی باشد. انواع مختلفی از شبیه سازی رایانه ای وجود دارد كه وجه مشترك همه آن ها در این است كه تلاش می كند تا یك نمونه از سناریوهای نمایانگر برای یك مدل تولید كنند كه در آن امكان محاسبه كامل تمام حالات ممكن مدل كه مشكل یا غیر ممكن بوده وجود داشته باشد.
به طور رو به افزونی معمول شده است كه نام انواع مختلفی از شبیه سازی شنیده می شود كه به عنوان « محیط های صناعی » اطلاق می شوند. این عنوان اتخاذ شده است تا تعریف شبیه سازی عملاً به تمام دستاوردهای حاصل از كامپیوتر تعمیم داده شود.
▪ شبیه سازی در علم كامپیوتر
در برنامه نویسی كامپیوتر، یك شبیه ساز اغلب برای اجرای برنامه ای مورد استفاده قرار می گیرد كه انجام آن برای كامپیوتر با مقداری دشواری همراه است. مثلاً، شبیه سازها معمولاً برای رفع عیب یك ریزبرنامه استفاده می شوند. از آن جایی كه كار كامپیوتر شبیه سازی شده است، تمام اطلاعات در مورد كار كامپیوتر مستقیماً در دسترس برنامه دهنده است و سرعت و اجرای شبیه سازی را می توان تغییر داد.
شبیه سازها همچنین برای تفسیر درخت های عیب یا تست كردن طراحی های منطقی VLSI قبل از ساخت مورد استفاده قرار می گیرند. در علم نظری كامپیوتر، عبارت شبیه سازی نشان دهنده یك رابطه بین سیستم های انتقال وضعیت است كه در مطالعه مفاهیم اجرایی سودمند می باشد.
▪ شبیه سازی در تعلیم و تربیت
شبیه سازی ها در تعلیم و تربیت گاهی مثل شبیه سازی های آموزشی هستند. آن ها روی وظایف خاص متمركز می شوند. در گذشته از ویدئو برای معلمین و دانش آموزان استفاده می شده تا مشاهده كنند، مسائل را حل كنند و نقش بازی كنند؛ هرچند یك استفاده جدید تر از شبیه سازی ها در تعلیم و تربیت شامل فیلم های انیمیشن است ( ANV ). ANV ها نوعی فیلم ویدئویی كارتون مانند با داستان های تخیلی یا واقعی هستند كه برای آموزش و یادگیری كلاس استفاده می شوند.ANV ها برای ارزیابی آگاهی، مهارت های حل مسئله و نظم بچه ها و معلمین قبل و حین اشتغال كارایی دارند.
شكل دیگری از شبیه سازی در سال های اخیر با اقبال در آموزش تجارت مواجه شده است. شبیه سازی های تجاری كه یك مدل پویا را به كار می برند، آزمون استراتژی های تجارت را در محیط فاقد خطر مهیا می سازند و محیط مساعدی برای بررسی موردی مباحث ارائه می دهند.
-
 مدیر بازنشسته
مدیر بازنشسته

اعداد حسابی
اعداد حسابی اعداد حسابی همان اعداد طبیعی هستند که صفر هم به آنها اضافه شده است. به عبارت دیگر به مجموعهی اعداد زیر ، اعداد صحیح یا اعداد درست گویند و آن را با Z نمایش میدهند: { ... , 3 , 2 , 1 , 0 , 1- , 2- , 3- , ...} = Z درواقع اعداد صحیح شامل اعداد طبیعی مثبت و اعداد طبیعی منفی و عدد صفر است. این اعداد همانند اعداد طبیعی جزء مجموعه های شمارش پذیر نامتناهی است. شاخه ای از ریاضیات که به مطالعه در مورد ویژگیهای اعداد صحیح می پردازدنظریه اعداد نام دارد. صحیح همانند اعداد طبیعی نسبت به اعمال جمع و ضرب بسته است،یعنی جمع و ضرب هر دو عدد صحیح، یک عدد صحیح است. و چون اعداد صحیح شامل اعداد منفی و صفر می باشند بنابراین بر خلاف اعداد طبیعی نسبت به عمل تفریق نیز بسته اند.ولی چون حاصل تقسیم دو عدد صحیح بر هم ممکن است عددی صحیح نباشد،پس نمیتواند نسبت به عمل تقسیم بسته باشد.
اعداد طبیعی
اعداد طبیعی، اعدادی هستند که برای شمردن به کار میروند. مجموعه اعداد طبیعی {... ,۳ ,۲ ,۱} است.
در این مجموعه عدد صفر وجود ندارد و با اضافه کردن آن، مجموعه اعداد حسابی به وجود میآید. این مجموعه یک
مجموعه نامتناهی است.
در ریاضیات، مجموعه اعداد طبیعی را با نماد N نمایش میدهند. این حرف از آغاز واژه انگلیسی Natural، به معنای
طبیعی، گرفته شده است.
اعداد اول
اعداد اول اعدادی طبیعی هستند که بر هیچ عددی بجز خودشان و عدد ۱ بخشپذیر نباشند. تنها استثنا عدد ۱ است که جزو این اعداد قرار نمیگیرد. اگرعددی طبیعی وبزرگتر از ۱ اول نباشد مرکب است.
عدد یکان اعداد اول بزرگتر از ۱۰ فقط ممکن است اعداد ۱، ۳، ۷، ۹ باشد.
اعداد اول جزو یکی از معماهای ریاضی باقیمانده است و هنوز کسی به فرمولی برای آنها به دست نیاورده است.
سری اعداد اول به این صورت شروع میشود: ۲، ۳، ۵، ۷، ۱۱، ۱۳، ۱۷، ۱۹ ...
قضیه ۱: تعداد اعداد اول بینهایت است.
برهان: حکم را به روشی که منسوب به اقلیدس است اثبات میکنیم: فرض کنید تعداد اعداد اول متناهی و تعداد آنها n تا باشد. حال عدد M را که برابر حاصلضرب این اعداد به علاوه ۱ را در نظر بگیرید. این عدد مقسومعلیهی غیر از آن n عدد دارد که با فرض در تناقض است.
قضیه ۲ (قضیه اساسی حساب): هر عدد طبیعی بزرگتر از ۱ را به شکل حاصلضرب اعدادی اول نوشت.
قضیه ۳ (قضیه چپیشف):اگر n عددی طبیعی و بزرگتر از ۳ باشد، حتما" بین n و ۲n عدد اولی وجود دارد. قضيه ۴ هر عدد زوج را میتوان بصورت جمع سه عدد اول نوشت.
قضيه ۵ هر عدد فرد (شامل اعداد اول) را میتوان به صورت جمع سه عدد اول نوشت (اثبات بر پايه قضيه ۴)
قضيه 6-هر عدد فرد را میتوان به صورت دو برابر يك عدد اول بعلاوه يك عدد اول ديگر نوشت.
خواص اعداد اول:
1- هر عدد اول برابر است با 6n+1 يا 6n-1 كه n يك عدد صحيح است.
2-مجذور هر عدد اول برابر است با 24n+1.
3-تفاضل مجذورهاي دو عدد اول مضربي از 24 است.
4-حاصلضرب هر دو عدد اول بجز 2و3 مضربي از 6 بعلاوه يا منهاي يك است.
توان چهارم هر عدد اول بجز 2و3 مضربي از 240 بعلاوه يك است.
بزرگترین عدد اول کشف شده برابر دو به توان ۳۰ميليون و ۴۰۲هزار و ۴۵۷منهاي يك است.این عدد یک عدد مرسن است. عدد مرسن عددی است که برابر 2 به توان n منهای یک است.
لازم به ذكر است كه تعداد 3000 عدد اول در سايت مگاسندر www.megasender.org وجود دارد و افرادي كه مايل به دريافت بيشتر اين اعداد هستند مي توانند با سايت مذكور تماس گرفته و تعداد بيشتري از آنها را بر روي لوح فشرده دريافت نمايند و طراحان اين سايت خودشان اين اعداد را محاسبه نموده اند
اعداد جبری
اعداد جبری در ریاضیات اعدادی هستند که جواب معادلهای به شکل زیر باشند:
anxn + an−1xn−1 + ··· + a1x + a0 = 0
ضریبهای a0 تا an در این معادله چند جملهای اعداد گویا هستند.
تمام اعداد گویا اعداد جبری هم هستند. بعضی از اعداد حقیقی عدد جبری نیستند. عددی که جبری نباشد عدد متعالی (یا غیرجبری) نامیده میشود.
اعداد حقیقی
میدان تمام اعداد گویا و گنگ را اعداد حقیقی گویند و آن را با R نمایش میدهند. اعداد حقیقی را میتوان با اضافه کردن عدد موهومی( ) بسط داد. اعدادی به فرم a + bi که در آن a و b هر دو عدد حقیقی هستند را اعداد مختلط مینامند.
اعداد صحیح
اعداد صحیح به مجموعهٔ اعداد طبیعی مثبت، اعداد طبیعی منفی، و عدد صفر گفته میشود. در ریاضیّات، معمولاً این مجموعه را با Z یا (ابتدای کلمه آلمانی Zahlen به معنی اعداد) نشان میدهند. همانند مجموعهٔ اعداد طبیعی، مجموعهٔ اعداد صحیح نیز یک مجموعهٔ شمارای نامتناهیست.
شاخهای از ریاضیّات که به مطالعهٔ اعداد صحیح میپردازد، نظریهٔ اعداد نام دارد.
خواص جبری
همانند اعداد طبیعی، Z نیز نسبت به دو عمل جمع و ضرب بسته است. این بدان معناست که حاصل جمع و حاصل ضرب دو عدد صحیح، خود، یک عدد صحیح است. بر خلاف مجموعهٔ اعداد طبیعی، از آنجا که اعداد صحيح منفی، و به ویژه، عدد صفر هم به Z تعلق دارند، این مجموعه، نسبت به عمل تفریق نیز بسته است. اما Z تحت عمل تقسیم بسته نیست، زیرا خارج قسمت تقسیم دو عدد صحیح، لزوما عددی صحیح نخواهد بود.
برخی از خواصّ اساسی مربوط به عملیّات جمع و ضرب در جدول زیر گنجانیده شده است (در اینجا b ،a، و c اعداد صحیح دلخواه هستند
جمع ضرب
بسته بودن: a + b یک عدد صحیح است a × b یک عدد صحیح است
شرکت پذیری: a + (b + c) = (a + b) + c a × (b × c) = (a × b) × c
تعویض پذیری: a + b = b + a a × b = b × a
وجود یک عنصر واحد: a + 0 = a a × 1 = a
وجود یک عنصر عکس: a + (−a) = 0
توزیع پذیری: a × (b + c) = (a × b) + (a × c)
نداشتن مقسوم علیههای صفر: اگر ab = 0، آنگاه a = 0 یا b = 0
مطابق بالا، خواصّ بسته بودن، شرکت پذیری و جابه جایی (یا تعویض پذیری) نسبت به هر دو عمل ضرب و جمع، وجود عضو همانی (واحد، یا یکّه) نسبت به جمع و ضرب، وجود عضو معسلامح فقط نسبت به عمل جمع، و خاصیّت توزیع پذیری ضرب نسبت به جمع از اهمیت برخوردارند.
در مبحث جبر مجرد، پنج خاصیّت اوّل در مورد جمع، نشان میدهد که مجموعهٔ Z به همراه عمل جمع یک گروه آبلی است. امّا، از آن جا که نسبتZ به ضرب عضو وارون (یا معسلامح) ندارد، مجموعهٔ اعداد صحیح، به همراه عمل ضرب، گروه نمیسازد.
مجموعهٔ ویژگیهای ذکر شده حاکی از این است که ، به همراه عملیّات ضرب و جمع، یک حلقه است، امّا، به دلیل نداشتن وارون ضربی، میدان نیست. مجموعهٔ اعداد گویا را باید کوچکترین میدانی دانست که اعداد صحیح را در بر میگیرد.
اگرچه تقسیم معمولی در اعداد صحیح تعریف شده نیست، خاصیّت مهمّی در مورد تقسیم وجود دارد که به الگوریتم تقسیم مشهور است. یعنی به ازاء هر دو عدد صحیح و دلخواه a و b) b مخالف صفر)، q و r منحصر به فردی متعلق به مجموعه اعداد صحیح وجود دارد، به طوریکه: a = q.b + r که در این جا، q خارج قسمت و r باقیمانده تقسیم a بر b است. این کار اساس الگوریتم اقلیدس برای محاسبه بزرگترین مقسوم علیه مشترک را تشکیل میدهد.
همچنین در جبر مجرد، بر اساس خواصی که در بالا ذکر شد، یک دامنه اقلیدسی است و در نتیجه دامنه ایدهآل اصلی میباشد و هر عدد طبیعی بزرگتر از یک را میتوان به طور یکتا به حاصلضرب اعداد اوّل تجزیه کرد (قضیه اساسی علم حساب.)
اعداد گویا
اعداد گویا1 حاصل تقسیم دو عدد صحیح بر یکدیگرست، به شرطی که عدد دوّم (مقسوم علیه) صفر نباشد. به بیان دیگر، هر عدد گویا را میتوان به شکل a/b یا آ بيم نوشت (که a و b اعداد صحیحاند).
در ریاضیات، مجموعه اعداد گویا را، عموماً، با Q نمایش میدهند. به عنوان مجموعهای شمارا (یا قابل شمارش)، ولی نامتناهی، مجموعهٔ اعداد گویا، خود، زیرمجموعهایست چگال (dense) از مجموعهٔ بزرگتر و عمومیتر اعداد حقیقی.
به عنوان یک اشتباه نسبتاً رائج، گاهی اعداد کسری را با اعداد گویا یکی میدانند. این در حالیست که، اعداد گویا فقط کسرهایی هستند که از تقسیم دو عدد صحیح حاصلآمده باشد. به عنوان نمونه، نسبت راديكال سه دوم کسر هست، ولی، گویا نیست.
اعداد مختلط
عدد مختلط عددی به فرم a + bi است که در آن a و b از اعداد حقیقی و i عدد موهومی برابر با ریشهٔ دوم عدد ۱- است.
اعداد مختلط از کجا آمدند
همان طور که میدانید یک معادله درجه دو مثل ax2 + bX + c = 0 در اعداد حقیقی وقتی که Delta = b2 − 4avc مقداری منفی باشد گوئیم جواب ندارد.این یعنی اداد حقیقی شمول همه اعداد نیست پس اعداد مختط تعریف شدد. عدد مختلط a + bi را میتوان به صورت (a,b) نوشت. برای اینکه مفهوم اعداد مختلط را نتوجه شوید ،ابتدا باید با اعداد مختلط آشنایی کامل داشته باشید. عداد مختلط: می خواهیم معادله را حل کنیم.این معادله درمجموعه های دارای جواب نیست. برای اینکه هیچ عددی بتوان 2 و به علاوه 1 صفر نمیشود.همچنین اگرعددی به توان زوج برسد،غیرممکن است که علامت آن منفی شود.«با به پشت مساوی بردن معلوم معادله(1+) می بینیم که مجهول عددیست که به توان رسیده ومنفی شده که محال است».اما باید گفت که اعداد را با علامت دیگری غیر از+و- شان میدهیم؛ آن علامت شامل اعداد مختلط و متناهی می شود. در اعداد متناهی این قانون هست که عددی با بتوان زوج رسیدن منفی هم بشود.این اعداد رابا علامت نشان می دهند. برای یک عدد حقیقی( )عدد متناهی را به صورت زیر نشان میدهند: اعدادی راکه دارای علامت i هستند را موهومی می گوئیم. پس باتوجه به مطالب فوق دریافته ایدکه:جواب معادله درمجموعه ی اعداد متناهی دارای دو جواب است: i,+i- اعداد متناهی: به نظر شما اگر دلتای معادله ی درجه دومی منفی بودچطور می توان ریشه معادله موردنظر را پیداکرد؟ می خواهیم معادله ی را حل کنیم. حل:
ازطرفی: ملاحظه می کنیم دو جوابی که بدست آمده اند بطورخالص نه حقیقی و نه موهومی به شمار می روند. لذاچنین اعدادی را در گروه اعداد مختلط جای دارند. یک عدد مختلط به صورت زوج مرتب :z=(x,y)معرفی می شوند.x: مولفه حقیقی و y: مولفه موهومی نام دارد. اعداد مختلط را می توان بصورت روبرو نشان داد: z=x+iy مزدوج آنر بصورت روبرو نشان می دهیم: 85.133.173.228 ۱۷:۲۸, ۱۹ ژوئیه ۲۰۰۶ (UTC) هرگاه مولفه های دو عدد مختلط دو به دو برابر بود؛آنرا؛دو عدد مختلط برابرنامیده می شود.
نکته:این اعداد همچون سایر مجموعه اعداد دارای خواصص توزیع پذیری،شرکت پذیری و جابجایی نیز هست.
میدان اعداد مختلط () میدان اعداد حقیقی () را به صورت زیر میدان، شامل میشود. درضمن z=(x,y) --->: x:مولفه حقیقی است و y:مولفه موهومی است.
اعداد مرکب
عدد مرکب عددی طبیعی بجز یک است که اول نباشد.
-
 مدیر بازنشسته
مدیر بازنشسته

مثلث خیام ، پاسکال بسیاری عقیده دارند که مثلث حسابی پاسکال را باید مثلث حسابی خیام نامید و برخی پا را از این هم فراتر گذاشته اند و معتقد اند که دو جمله ای نیوتون را باید دوجمله ای خیام نامید . اندکی در این باره دقت کنیم.
همه کسانی که با جبر مقدماتی آشنایی دارند ،"دستور نیوتن" را درباره بسط دوجمله ای میشناسند. این دستور برای چند حالت خاص (وقتی n عددی درست و مثبت باشد) چنین است:
(a+b)0 = 1 (1)
(a+b)1 = a+b (1,1)
(a+b)2 = a2+2ab+b2 (1,2,1)
(a+b)3 = a3+3a2b+3ab2+b3 (1,3,3,1)
(a+b)4 = a4+4a3b2+6a2b2+4a2b3+b4 (1,4,6,4,1)
. . .
اعداد داخل پرانتزها، معرف ضریبهای عددی جمله ها در بسط دوجمله ای است.
بلیز پاسکال (Blaise Pascal) فیلسوف و ریاضی دان فرانسوی که کم وبیش با نیوتون همزمان بود، برای تنظیم ضریبهای بسط دوجمله ای، مثلثی درست کرد که امروز به "مثلث حسابی پاسکال" مشهور است. طرح این مثلث برای نخستین بار در سال 1665 میلادی در "رساله مربوط به مثلث حسابی "چاپ شد.مثلث حسابی چنین است:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
دراین مثلث از سطر سوم به بعد هر عددبرابر با مجموع اعداد بالا و سمت چپ آن در سطر قبل است و بنابراین میتوان آنرا تا هر جا که للازم باشدادامه داد. هرسطر این مثلث ضریبهای بسط دوجمله ای را در یکی از حالتها بدست میدهد بطوری که n همان شماره سطر باشد.
ضریبهای بسط دوجمله ای (برای توانهای درست و مثبت) حتا در سده دوم پیش از میلاد البته به صورت کم و بیش مبهم برای دانشمندان هندی روشن بوده است .باوجود این حق این است که دستور بسط دو جمله ای با نام نیوتن همراه باشد زیرا نیوتن آن را برای حالت کلی و وقتی n عددی کسری یا منفی باشد در سال 1676میلادی بکاربرد.که البته در این صورت به یک رشته بی پایان تبدیل میشود.
اما در باره مثلث حسابی وضریبهای بسط دوجمله ای در حالت طبیعی بودن n. از جمله، دستور بسط دو جمله ای را میتوان در "کتاب حساب مخفی" میخائیل شتیفل جبردان آلمانی (که در سال 1524 چاپ شد) پیدا کرد.
در سال 1948 میلادی،پاول لیوکی آلمانی،مورخ ریاضیات،وجود دستور نیوتن را برای توانهای طبیعی ،دز کتاب "مفتاح الحساب"(1427 میلادی) غیاث الدین جمشید کاشانی کشف کرد. بعدها س.آ.احمدوف ،مورخ ریاضیات و اهل تاشکند، دستور نیوتون وقانون تشکیل ضریبهای بسط دوجمله ای را،در یکی از رساله های نصر الدین توسی،ریاضیدان بزرگ سده سیزدهم میلادی ،کشف کرد (این رساله توسی درباره محاسبه بحث میکند). چه جمشید کاشانی وچه نصرالدین توسی ،این قاعده را ضمن بررسی قانون های مربوط به ریشه گرفتن از عددها آورده اند.
همچنین براساس آگاهی هایی که داریم حکیم عمر خیام رساله ای داشته که خود رساله تاکنون پیدا نشده ولی از نام آن "درستی شیوه های هندی در جذر وکعب "اطلاع داریم ،کهدر آن به تعمیم قانونهای هندی درباره ریشه دوم و سوم ،برای هر ریشه دلخواه پرداخته.لذا خیام از "دستور نیوتن" اطلاع داشته.
اما بنا به اسناد تاریخی معتبر قانونهای مربوط بهضریبهای بسط دوجمله ای وطرح مثلث حسابی تا سده دهم میلادی(برابر چهارم هجری) جلو میرود و به کرجی (ابوبکر محمد بن حسن حاسب کرجی ریاضیدان سده ده و یازده میلادی) پایان میپذیرد .بنابراین حتی" مثلث حسابی پاسکال" را هم از نظر تاریخی نمیتوان "مثلث حسابی خیام " نامید.
-
 مدیر بازنشسته
مدیر بازنشسته

اهرام مصر اهرام از زبان لوموند
كهن ترين بنايي كه در پرده اي از ابهام پوشيده شده و هنوز باقي مانده است ، با كليه پيشرفتهاي علمي و تكنولوژي در دنياي امروز، باز هم اعصار مجهول تاريخ از نظرها به دور مانده است . هنور حتي انسان نمي تواند به دقت قديم و آثار قديمي ،سنگهاي ساختماني را با همان ظرافت بسازد . هنوز استادان از روي هم چيدن سنگهايي به قطعات هفتاد تن مشابه آنچه كه با دقت و وسواس عظيم در بناي هرم بزرگ به كاررفته است ، عاجزند . هنوز محاسبات رياضي ما در اندازه گيري ابعاد زمين و حركت سياره ها از دقت و صحت محاسبات انجام شده در زمان بناي هرم بزرگ برخوردار نيست . اينكه چرا هنوز در تهيه و تدارك وسايل اندازه گيري لنگان لنگان به دنبال انسانهاي ماقبل تاريخ هستيم ، چگونه اين تمدن درخشان ، هرمهاي مصر ، در برهه اي از زمان درخشيده و سپس ناپديد شده است ، بر ما پوشيده مي باشد . هنوز كاملأ مشخص نيست كه آيا اين قدرت علمي و هنري كه انسان امروز تنها گوشه اي از آن را دريافته است ، از يك مغز فوق انسان و يا منبع فكري خارق العاده است . اين امكان را هم مذهب و عرفان تاييد مي كند . امكان ديگر رسيدن اين تمدن پيشرفته از خارج كره زمين به ساكنان زمين است و يا البته لزومأ نمي توان گفت كه يكي از اين نظريات درست است . با توجه به آنكه بشر امروز هنوز در تنگناي اين تمدن سردرگم است و مي انديشد كه اين اين امر يك مسئله خارق العاده و خاص مي باشد و لذا سبب آن نيز خاص است ، در هر حال منبع و منشا اين ظرافت هنري و علمي در ساختمان هرم بزرگ و اهرام مصر هرچه باشد ، اين حقيقت به جاي خود باقي است كه اين ساختمان از چنان نبوغ و مهارت شگرفي برخوردار است كه در طول تاريخ انسان ها نظير آن مشاهده نشده است و هر جسم يا ساختمان هرمي شكل كه دقيقأ با ابعاد متناسب با هرم بزرگ مصر ساخته شود و در امتداد شمال و جنوب ميدان مغناطيسي زمين قرار گيرد ، مي تواند به پيرايش ، انعكاس و تمركز ميدان هاي انرژي منتهي شود . از آزمايش هاي متعددي كه در درون اجسام هرمي شكل با ابعاد چند سانتي متر يا چند متر انجام شده ، اين نتيجه حاصل گرديده است كه نوع جسم يا ماده اي كه در ساختمان اين اهرام به كار مي رود ، به هيچ وجه در ماهيت ميدان هاي انرژي كه در درون آن ها متمركز مي شود ، تاثير ندارد .
"نتايج آزمايش هاي انجام شده "
1- غذاهاي فاسد شدني تا مدتها مديد بدون فساد در درون هرم باقي مي ماند
2- آب هاي آلوده ، تصفيه و عاري از ميكروب مي شوند *در مورد اين ازمایش در فصول آينده بيشتر صحبت خواهيم كرد
3- نباتات با سرعت بيشتري رشد مي يابند
4 - فلزات زنگ زده ، جلا و صيقل اصلي خود را باز مي باند
5 - انسان ها به استراحت بهتري دست يافته و نيز به قدرت انديشه آدمي افزوده مي شود
6- آرامش و درمان امراض رواني با سهولت بهتري انجام مي شود
مسئله اي كه براي اولين بار منتهي به كشف اين خواص در اجسام هرمي شكل گرديده ، ملاحظه اين حقيقت بود كه حيوانات مرده در اندرون آرامگاه اصلي فرعون در هرم بزرگ هرچند آب خود را از دست داده ولي فاسد نشده اند در نتيجه اين مشاهده بود كه بشر متوجه گريد كه شايد شكل خاص هرم در اين پديده دخالت داشته باشد . براي تحقيق اين موضوع هرمي به ارتفاع75 سانتيمترساختند و جسد يك گربه را مستقيمأ در زير راس هرم و به فاصله يك سوم ارتفاع هرم از پايه آن قرار دادند و مشاهده كردند كه گربه چندي بعد بدون هرگونه تجزيه و فساد به مومياي تبديل شده است . در آخر نتايج اين آزمايش منشر شد ، اعلام گرديد كه بين شكل اهرام و اثرات فيزيكي و شيميايي و بيولوژي فضاي داخل آن نسبت هاي معيني وجود دارد و با رعايت اين نسبت ها مي توان اثرات ناشيه را تشديد نمود .
بر خلاف تصور عمومي كه به مدت 500 سال هرم گيزا را تنها آرامگاهي بزرگ براي خئوپس تصور مي كرد و دستور ساخت آن را تنها علت عقده هاي خود بزرگ بيني مي دانست ، اكنون دانشمندان دريافته اند كه اين بناي شگفت انگيز ، گنجينه اي از علوم مهندسي ، رياضي ، ژئودزي ، اختر شناسي ، معماري و ديگر دانش هاي شناخته شده روزگار خود ما بوده است . گويااين ساختمان هرمي شكل همچون كتابي سنگي بازگو كننده دانش و تكنولوژي آن روزگاران است .
مورخين ، جهانگردان و دانشمندان عليرغم وجود اهرام بي شماري كه در سرتاسر زمين (چين ، ژاپن ، مصر ، .. ) هست . تنها در زمينه هرم گيزا بوده است كه كتابها نوشته اند و پژوهش ها كرده اند ، به عنوان مثال در مصر حدود 30 هرم نسبتأ مهم وجود دارد كه از نظر محققان 6 هرم كه قبل از هرم بزرگ ساخته شده است ، از نظر عظمت ، كمال هندسي و محاسبات رياضي در سطح پايين تر قرار دارند و در 23 هرم ديگر كه پس از آن ساخته شده اند ، از دقت و ظرافت كار به نحو محسوسي كاسته شده است
هرم بزرگ در 16 كيلومتري غرب قاهره در زمين مسطحي به وسعت 6/2كيلومتر مربع از دشت جيزه مشرف به نخلستانهاي دره نيل بنا گرديده و سطح زير بناي آن كه اندكي بيش از 13 جريب را مي پوشاند با دقتي معادل چند ميليمتر اختلاف تسطيح شده است
دانشمندان پر آوازه جهان در پي مطالعه و محاسبات گسترده خود به اين نتيجه شگفت انگيز دست يافته اند كه ابعاد هرم گيزا در رابطه تنگاتنگ با ابعاد كره زمين است . يعني نه تنها طول پيرامون قاعده هرم برابر طول نيم دقيقه قوس نصف النهاري است كه از راس هرم گذشته و دلتاي رود نيل را در بر ميگيرد ،بلكه دانش نوين پيراميدوگرافي ثابت كرده است كه بسياري از ابعاد بنيادين بخش هاي گوناگون هرم گوياي شمار روزها ، سالها و سده هاي شمسي اند
ولي متاسفانه نحوه محاسبه اين اعداد در حدود 6800 سال قبل هنوز مشخص نشده است ، همچنين مداركي كه سطح جنوبي هرم يافت شده است كه ثابت مي كند مصريان از اين سطح به وسيله پديده اي كه فلاش نام گرفته ، روزهاي تعديل بهاري و پاييزي را تعيين مي كرده اند . افزون بر اين نور انقلاب زمستاني نيز توسط گوي زريني كه دو راس هرم قرار داشته اعلام مي نمودند .
براي ساختمان اين اهرام ، دو ميليون و ششصد هزار قطعه ، سنگ هاي ساختماني تراشيده شده ، از گرانيت و سنگ مرمر با وزن هايي از 2 تا 70 تن با دقتي بي مانند در حدود جزئي از ميليمتر تراشيده شده تا بنايي به ارتفاع 140 متر پديد آورده است . نكته جالب اينكه در احداث زاويه ها و شيب هاي هرم ، عامل دقيق و پيشرفته علم مثلثات مورد نظر بوده است . تسطيح و هموار كردن چندين هزار هكتار زمين دشت جيزه براي زيربنا و محوطه پيرامون هرم و نيز تراش و صيقل دادن آن قطعات عظيم سنگي ، چنانچه از برگردان حروف هيروگريف منقوش بر سنگ نوشته ها و همچنين از گفته هاي كاهنين به هرودوت (پدر تاريخ)بر مي آيد ، مصريان پستي و بلندي هاي مسطح زيرپي را به وسيله آب ، هموار و محوطه را تسطيح و تراز مي كردند . مجموعه اطلاعات به دست آمده تا امروز حاكي از اين است كه هرم بزرگ ، راز بزرگ يك دانش گمشده در تاريخ را در سينه خود دارد .تاچندي پيش هرگونه دليل روشني وجود نداشت كه مصريان پنج هزار سال پيش توانايي محاسبات رياضي و نجومي دقيق براي پايه گذاري اين چنين ساختمان شگفت آوري را داشته اند .
" برخي از مشاهدات درمورد هرم "
بسياري سال پيش ، گروهي از مردم به طور اتفاقي متوجه شدند كه صداهاي غير عادي به مانند زمزمه هاي نامفهوم از اهرام به گوش مي رسد . با توجه به آنكه صدا و صوت نوعي انرژي است ، اگر مصر قديم به خواص و آثار مرتبت بر صدا تا اين حد آشنايي داشتند ، كاملأ منطقي به نظر مي رسد كه جنبه هاي اكوستيك معماري در ساختمان هرم رعايت كرده باشند و حقايق مشهود نيز اين گمان را تاييد مي كند . در تمدن و فرهنگ ملل قديم به خصوص در افسانه هاي ملت چين مكرر از نوعي نداسنگ ، يافت مي شود . اين سنگ ها از نوع يشم بوده و به هنگام برخورد دو قطعه از آنها ، آوايي خوش شبيه به آهنگ موسيقي شنيده مي شود . چيني ها اين طنين را صدايي آسماني و نداي بزرگ طبيعت مي ناميدند
سر ويليام ، دويست سال قبل يك خبرنگار كنسول الجزيره در گالري بزرگ اهرام هرم گيزا ، براي اولين بار متوجه شد كه صدا در اين فضا به وجهي غير عادي تشديد و طنين انداز مي شود ، اما چنانكه بعد ها مشخص شد ، اين تشديد صدا محدود به هرم بزرگ نيست . بسياري از افراد ادعا كرده اند كه صداهايي غيرعادي به مانند زمزمه هاي نا مفهوم كه از راه دور به گوش مي رسيد از هرم هاي كوچك (مدل) نيز شنيده اند . از زمانهاي بسيار قديم ، پزشكان به اين حقيقت آشنا بودند كه صداي موسيقي در شفاي پاره اي امراض به خصوص بيماريهاي رواني اعجاز مي كند . رشد گياهان را سرعت مي بخشد و در حيوانات و انسانهايي كه در معرض انواع صدا قرار مي گيرند ، تغييرات و تحولات كاملأ محسوسي پديد مي آورد و اينك بر اساس دانش جديد همه اين پديده ها نشانگر آن است كه امواج صدا حامل نوعي انرژي هستند كه عميقأ بر روي سلولها اثر مثبا يا منفي باقي مي گذارند . در مصر قديم ، صدا به عنوان يكي از ابزارهاي اصلي براي درمان بيماريها به كار گرفته مي شد . يونانيان ، ايرانيان ، هنديها، سرخپوستان آمريكا و بسياري از قبايل بدوي از اين سيستم معالجه سود مي گرفتند .فيثاغورث حكيم يوناني در مورد آزمايش هاي خود از صدا به عنوان يك نيروي خلاق نام ميبرد كه ارتعاشات آن هم جنبه مادي و فيزيكي و هم اثرات معنوي دارد . او مدعي بود كه اين علم را در انجمن ها ي سري مصر فراگرفته است .يكي از جالبترين تجربيات در مورد تاثير صدا به وسيله خانم دورتي رتالاك همسر يك موسيقيدان به عمل آمده است
" شعاعهاي نوراني اهرام "
گزارشهاي ديگر درباره هرم بزرگ حاكي است كه گهگاه شعاع هاي نوراني دايره اي شكل ، اطراف هرم را در بر مي گشود و يا صدا هايي ناله مانند از پيكره ابوالهول شنيده مي شود . به هر صورت طبيعت انرژي در اطراف و داخل هرم هرچه تصور شود و هدف سازندگان و معماران آن در ايجاد و كاربرد قدرت هاي كيهاني هرچه بوده باشد ، اين حقيقت به جاي خود باقي است كه هم اكنون اين نيرو ها در هرم حضور دارند و زماني كه به شناسايي و نحوه عمل اين نيروها آگاه شويم شايد به استقرار تمدني بنيادي و اصولي توفيق فراهم يافت .
يكي از نويسندگان به نام پيتر تامكينز به نقل از سر ويليام سيمونز يكي تز مخترعين انگليسي مي گويد :در مسافرت به مصر و بازديد از هرم گيزا هنگاميكه در فضاي باز راس هرم ايستاده بودم ، بر حسب تصادف دستهاي خود را به طرف بالا بردم و دريافتم كه با حركت انگشتانم ، صداي تخليه الكتريسيته استاتيك از خازني به گوش مي رسد . آن گاه تنها انگشت اشاره دستم را به طرف بالا بردم و حالتي همانند سوزن سوزن شدن ، در انگشتم احساس نمودم . در اين حالت بر آن شدم جرعه اي از شرابي كه به همراه داشتم بنوشم ولي با نزديك نمودن بطري به لبانم ناگهان يك شوك الكتريكي ايجاد گرديد . به دنبال كشف اين پديده تدبير جالبي انديشيده و يك روزنامه را به آب آغشته نمودم . سپس آن را همانند لفافي به دور شيشه شراب پيچيده و بدين سان بطري را به يك خازن الكتريسيته تبديل نمودهم ، آنگاه بطري را در بالاي سر خود نگاه داشتم . در اين حال به روشني صداي تخليه الكترسيته استاتيك به گوش مي رسيد . سر ويليام مي افزايد : سپس به يكي از همراهان نزديك شده و دست او را لمس نمودم ، در اين حالت شوك الكتريكي شديدي ايجاد شد به گونه اي كه وي ناگزير به گريختن از راس هرم گرديد
" بمباران اتمی اهرام "
سال 1961 ميلادي را مي توان سرآغاز دگرگوني در بررسي اسرار هرم گيزا دانست . . در اين سال دكتر لويي الوارز، برنده جايزه نوبل در رشته فيزيك بر آن شد كه اسرار درون هرم گيزا را كشف نمايد . وی بر این باور بود كه اين بار با روشي كاملأ نوين و جدا از شيوه هاي آزموده شده پيشين احتمالأ بتواند به اسرار نهفته در سردابها و اتاق هاي پنهاني درون آن راه يابد . در اين هنگام كه شايد از صدها پژوهشگر اهرام ازسراسر جهان با بي صبري در انتظار پايان آزمايشها و اعلام نتيجه نهايي بودند بمباران اهرام بيش از 2 ميليون بار توسط دكتر كهد كه همكار دكتر الوارز ، آغاز گشت . ليكن با نهايت تاسف و ناباوري پس از تجزيه و تحليل نتايج به دست آمده توسط كامپيوتر هاي پيشرفته دانشگاه قاهره پاسخي كه انتظار مي رفت به دست نيامد . پس از سپري شدن نزديك به يك سال از بمباران اهرام توسط دانشمندان ياد شده ، يكي از خبرنگاران روزنامه تايمز لندن به نام جان تامن تف در نوشتاري كه در 14 جولاي 1969 در اين روزنامه به چاپ رسيد گفت اهرام تمامي قوانين شناخته شده دانش فيزيك را رد مي كند ، زيرا متاسفانه هر بار نتيجه به دست آمده آزمايش را به كامپيوتر داده ايم پاسخي كاملأ متفاوت با پاسخ هاي پيشين دريافت داشته ايم . دكتر كهد مسئول طرح بمباران اهرام نيز در پاسخ به نوشتار خبرنگار انگليسي مي گويد : اينك ناچاريم يكي از اين دو فرضيه زير را بپذيريم
یک - با توجه به شكل هندسي و ابعاد و موقعيت جغرافيايي اهرام ، احتمالأ نيروهاي مرموز و نا شناخته اي در كارند كه مانع انجام عمليات شده و يا به گفته ديگر سردرگمي كامپيوتر ها را موجب مي شوند
دو - برابر پيش بيني هاي به عمل آمده از سوي فراعنه در هزاران سال پيش همچنين به باور اهالي بومي دشت گزا ، گرفتار نفرين فراعنه آرميده در درون اهرام ميشویم
محققان : آقايان بهنام جهاني و سياوش شير عليان
پژوهش سراي دانش آموزي ناحيه 7 انجمن رياض
-
 مدیر بازنشسته
مدیر بازنشسته

پنجه یعنی پنج انگشت نگاهی به پیشرفت شمارش و محاسبه در طول تاریخ
كهن ترین وسیله محاسبه كه انسان در طبیعت و در طول تاریخ با آن سروكار داشته است، دست های او بوده است. مفهوم عدد و شكل از جایی جز جهان واقع گرفته نشده است؛ «ده انگشت دست كه انسان شمردن و محاسبه را به یاری آن انجام می داد.»
نام بسیاری از عددها در زبان های مختلف روشن می كند كه وسیله نخستین بشر برای محاسبه انگشتان او بوده است. در زبان فارسی به پنج انگشت دست «پنجه» می گویند. در واقع عدد پنج در بسیاری از قوم ها، مبنای شمارش بوده است و در بین بسیاری از قوم ها محاسبه با انگشتان دست و گاهی پاها تكامل یافته است.
حتی یك نویسنده به نام «به وا داستان پوج ته نی» در نوشته او در تمام سده های میانی مورد استفاده بوده و امروز استفاده از انگشتان دست در برخی جاها معمول است. «كارپینكی» تاریخ نویس ریاضیات در كتاب «تاریخ حساب» خود به این مطلب اشاره می كند كه در محل بورس بزرگ غله در شیكاگو همه قیمت ها به وسیله دلا ل ها با انگشتان محاسبه می شود.
همین انگشتان بود كه عددشماری در مبنای پنج (یك دست) در مبنای ده (دو دست) و در مبنای ۲۰ (انگشتان دست ها و پاها) را به وجود آورد. در میان بسیاری از ملت ها، محاسبه با انگشتان پیشرفت زیادی كرده بود. در «اودیسه هومر» بارها به جمله «به پنج درآوردن» برمی خوریم كه به معنای «محاسبه كردن» به كار رفته است و نشان می دهد كه در زمان هومر، محاسبه با انگشتان معمول بوده است. در یكی از كمدی های آریستو فان آمده است: «من همه مالیات ها را، بدون سنگ ریزه با دست هایم و به سادگی محاسبه كردم.»
در برخی نقاط هم از وسیله ای برای محاسبه استفاده می كردند كه از چوب درست شده بود و شكاف هایی داشت. نخستین نوشته های عددی به صورت نقش های برجسته ای در نقاشی های معبد فرعون «سه تی اول» «در آبی دمس» مربوط به نزدیك به ۱۳۵۰ سال قبل از میلاد دیده می شود. در این نقش ها یكی از خدایان مصری نشان داده شده كه حكومت فرعون را روی شاخه ای از نخل مشخص می كند.
در سده های بعد، از چوب خط برای محاسبه و گردآوری مالیات استفاده می كردند. چوب خط به دو بخش طولی تقسیم می شد كه یكی نزد دهقان و دیگری نزد حساب دار مالیاتی می ماند. این روش محاسبه مالیاتی در انگلیس تا سده هفدهم رایج بود. یك بار دهقانان انگلیسی برای از بین بردن تعهد های مالیاتی عقب مانده خود در بیرون اداره مالیات، خرمنی از چوب خط ها جمع كرده و سپس آن را آتش زدند. این خرمن چنان بزرگ بود كه خود ساختمان اداره مالیات را هم به آتش كشید. در این آتش سوزی نمونه مقیاس های انگلیسی طول هم از بین رفت، به نحوی كه از آن به بعد انگلیسی ها مقدار دقیق «فوت» (= پا) را نمی دانستند.چینی ها، هندی ها و بومیان پرو برای نشان دادن عدد از گره روی ریسمان استفاده می كردند. در آمریكا پیش از ***** اروپایی ها هر نماینده دولتی از این ریسمان های گره دار با خود داشت.
بومیان پرو برای محاسبه مجموعه ای از پنج ریسمان در اختیار داشتند كه روی چهارتای آن مقدارها با گره هایی معین شده بود و روی پنجمی مجموع آنها و باز هم به كمك گره مشخص می شد.
با پیشرفت تولید و آغاز داد و ستد دیگر چوب خط و ریسمان گره دار نمی توانست نیاز روزافزون محاسبه را برآورده كند. تكامل عددنویسی هم با دو مانع روبه رو بود. نخست اینكه وسیله مناسبی برای انجام محاسبه ها وجود نداشت. ورقه های گلی و مومی برای این منظور مناسب نبود. استفاده از پوست تازه در سده پنجم پیش از میلاد كشف شد و در ضمن خیلی گران بود. كاغذ خیلی دیرتر كشف شد. (برای نمونه، در اروپا، از سده یازدهم) دوم آنكه با توجه به دستگاه عددنویسی آن زمان، انجام عمل های حسابی بسیار دشوار بود. تلاش برای ضرب دو عدد LXXIV و CLVI در دستگاه عددهای رومی بسیار بی نتیجه به نظر می رسد! همین دشواری ها بود كه موجب پدید آمدن وسیله ای برای محاسبه شد كه آن را چرتكه (Abaq) می گفتند.
ریشه واژه «آباك» چندان روشن نیست. به عقیده برخی از تاریخ نویسان «آباك» به معنای تخته ای پوشیده از شن نرم است. در واقع هم شكل نخستین آباك، تخته مستطیل شكلی بوده است كه روی آن را با خاك یا شن نرم پوشانده بودند و با چوب نوك تیزی روی آن شكلی كه را می خواستند می كشیدند. ارشمیدس روی یكی از همین چرتكه های ماسه ای سرگرم محاسبه بود كه سربازی رومی وارد اتاق او شد. ارشمیدس از او خواست به شكلی كه رسم كرده است دست نزند و سرباز او را كشت!
چرتكه اولین ماشین پیشرفته برای كمك به انجام عملیات ریاضی است. نخستین چرتكه حدود سه هزار سال پیش از میلاد به وسیله شخصی ناشناس ساخته شد. چرتكه مدل های مختلفی داشت، اما معمول ترین آن چرتكه چینی بود؛ اسباب ساده ای برای محاسبه متشكل از مهره هایی كه به سیم ها یا میله هایی كه در قابی جایگزین شده است، كشیده شده و هر دسته از مهره ها نماینده مرتبه ای از اعداد است. چرتكه ای كه میان ایرانیان، ارامنه، عرب ها و ترك ها رایج است شباهتی به چرتكه چینی و چرتكه هایی كه در اروپای غربی رایج بود، ندارد و احتمالاً به وسیله محاسبان ایرانی یا عرب اختراع شده است و بعدها از كشورهای اسلامی به روسیه رفته است.
به گواهی هرودوت (سده پنجم پیش از میلاد) مصری ها از چرتكه استفاده می كردند. آنها برخلاف یونانی ها، سنگ ریزه ها را به جای از چپ به راست از دست راست به چپ جابه جا می كردند و به این ترتیب در زمان هرودوت هم در یونان و هم در مصر به طور گسترده از چرتكه استفاده می كردند. به احتمال زیاد یونانی ها روش استفاده از چرتكه را ضمن داد و ستد از فینیقی ها آموختند. آنها سنگ ها را در ستون های مختلف برحسب ارزش پولی قرار می دادند.
مردم قدیم «آباك» را «كالكولی» یا Colcule می گفتند و آن را با سنگ، استخوان یا شیشه می ساختند. واژه كالكولی به معنای سنگ ریزه بود و از همین واژه بعدها واژه لاتینی «كالكولاس» (Calcullus) به معنای «حساب» و «محاسبه» هم از همین كلمه مشتق شده اند. از این تخته های محاسبه تنها یكی باقی مانده است و آن مستطیلی است كه در جزیره «سالامیس» پیدا شده است.
سرچشمه چرتكه امروزی معلوم نیست ولی مسلم است كه یونانی ها آن را نداشته اند. عددنویسی ده دهی امروزی ریشه هندی دارد ولی محمد خوارزمی ریاضیدان ایرانی سده نهم میلادی در كتاب «حساب هندی» خود موجب رواج آن در اروپای مغرب زمین (البته به تدریج و به كندی) شد.
در این روش نوشتن عددها با ده رقم از صفر تا ۹ می توان همه عددها را نوشت. به جز آن این روش بر اصل موضعی بودن رقم ها استوار است. چرتكه در زمان ما چندان مورد استفاده ندارد، ولی نابینایان می توانند به خوبی از آن استفاده كنند
کلمات کلیدی این موضوع
 مجوز های ارسال و ویرایش
مجوز های ارسال و ویرایش
- شما نمیتوانید موضوع جدیدی ارسال کنید
- شما امکان ارسال پاسخ را ندارید
- شما نمیتوانید فایل پیوست کنید.
- شما نمیتوانید پست های خود را ویرایش کنید
-
مشاهده قوانین
انجمن








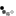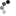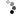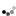
 پاسخ با نقل قول
پاسخ با نقل قول